Linear equations in two variables

Example 9
Complete Table 6 with solutions to the equation 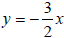. Then graph the solutions and show that
they are collinear.

Definition
An equation that can be written in the form Ax + B y = C (not both A and B zero) is called a
linear equation of x and y . The graph of all of the solutions to a linear equation with two
variables is a (straight) line (when graphed in the rectangular coordinate plane).
Three or more points in the plane are collinear (lie on a common line) if and only if they all
satisfy a common linear equation.

Example 10
Complete Table 7 with four solutions to the equation x + 2 y = 6. Then graph the solutions and
show that they are collinear.

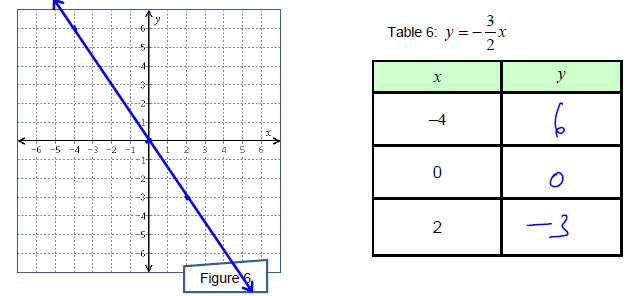
Example 11
Complete Table 8 with four solutions to the equation 3 x − 2 y = 6. Then graph the solutions and
show that they are collinear.

Definition
When a line or a curve is drawn in the xy-plane, any point on the line or curve that also lies on the
y-axis is called a y-intercept and any point on the line or curve that also lies on the x-axis is
called an x-intercept .
x-intercept: (x,0) y-intercept: (0, y)

Example 12
State all of the intercepts of the curve shown in Figure 9.

Example 13
Find the intercepts of the line with equation 3x − 5 y = − 20 .

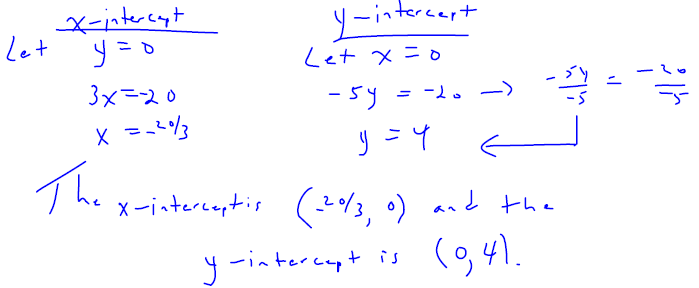
Example 14
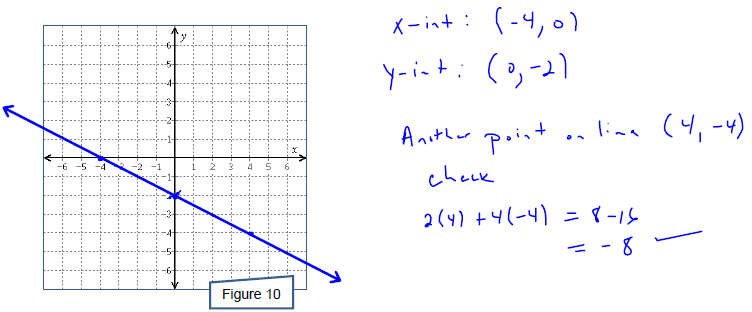
Plot the line 2 x + 4 y = − 8 onto Figure 10 after first finding the intercepts of the line. Find a
third point on your plotted line and show that it also satisfies the equation.

Example 15
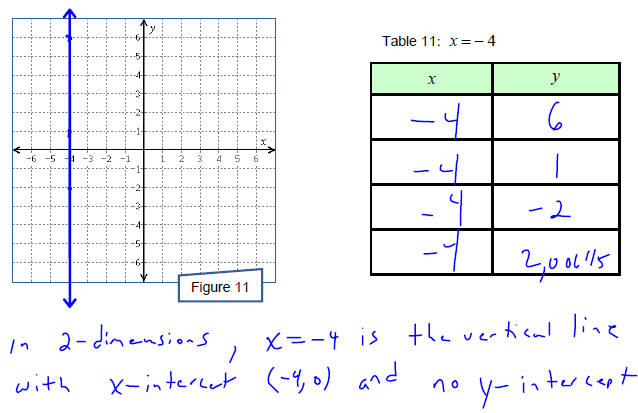
Plot onto Figure 11 several points in the xy-plane that satisfy the equation x = − 4 . What do you
observe? What are the intercepts of the resultant curve?

Example 16
What is an equation for the line in Figure 12? What are the intercepts of the line?
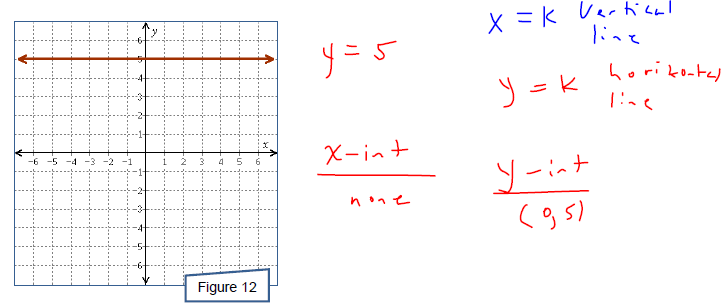