Rational Expressions and Functions
11.1 Simplifying Rational Expressions
1) A rational expression is simply the quotient of two polynomials. See examples
presented in this section.
3)
a) The expression is undefined at 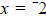 because
substitution of because
substitution of 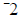 into the into the
expression will yield a denominator of zero. Division by zero is undefined.
b) Y = (X – 3)/(X + 2)
c) When 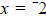 , Y1 the calculator reads ERROR. , Y1 the calculator reads ERROR.
5)
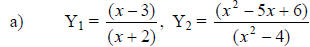
Table results:
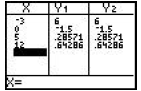
b) The expressions are not equivalent at x = 2 because
substitution of 2 for x
in both expressions yield different output values.
For x = 2,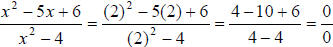 ,which is ,which is
undefined. For x = 2,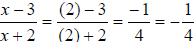 . .
7)
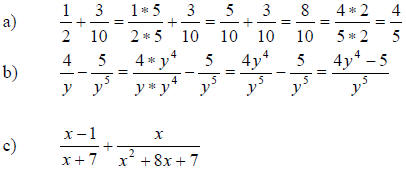
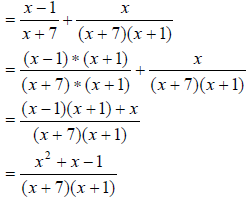
9)
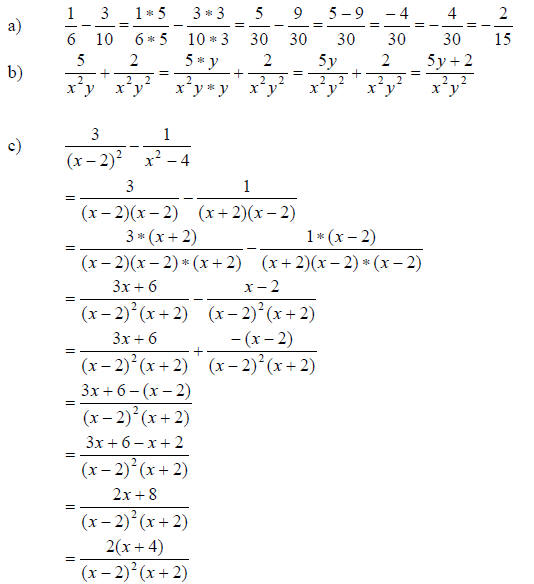
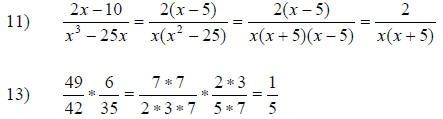
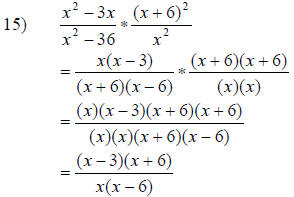
Skill and Review
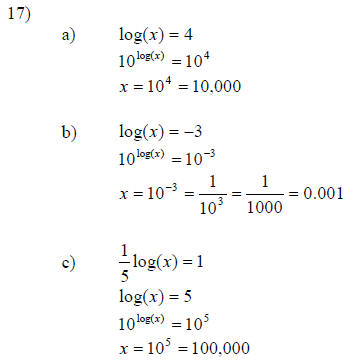
19)
a) 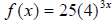 is an exponential growth function. This
is because the is an exponential growth function. This
is because the
function is of the form 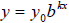 with b > 1 and k >
0. One could with b > 1 and k >
0. One could
conclude the graph of f is a growth function by observing that as x takes
on larger values, the value of the function f(x) increases.
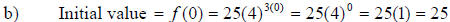
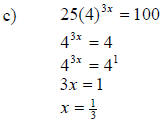
|