Solving Exponential and Logarithmic Equations
Here we will make use of what we have learned about
exponentials and logarithms to solve equations.
One-to-One Property of Exponential Functions –
If b^n = b^m then n=m |
We may make use of the above property if we are able to
express both sides of the equation in terms of the same base as shown here.
| |
Solve 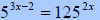 |
Recall the rule of exponent
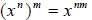 |
| |
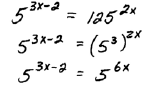 |
Step 1: Express both sides in terms of the same
base. |
| Step 2: Equate the exponents. |
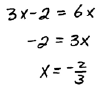 |
Step 3: Solve for the variable. |
A. Solve
It is not always the case that we will be able to express
both sides of an equation in terms of the same base. For this reason we will
make use of the following property.
One-to-One Property of Logarithmic Functions –
For all real b, b > 0 and b ≠ 1
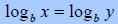 if and only if x = y if and only if x = y |
| |
Solve 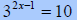 |
|
| Step 1: Take the common log of both
sides. |
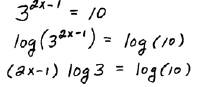 |
Step 2: Apply the power rule for logarithms |
| Step 3: Solve for the variable. |
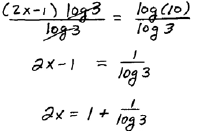 |
|
| Exact Answer |
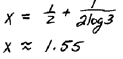 |
Approximate answer rounded off to the nearest
hundredth. |
B. Solve
When solving exponential equations and using the above
process the rule of thumb is to choose the common logarithm unless the equation
involves e. We choose these because there is a button for them on the
calculator. But certainly we could use any base we wish; this is the basis for
the derivation of the change of base formula.
| |
Prove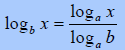 |
|
| Step 1: Apply the definition of the logarithm. |
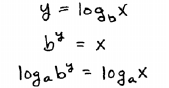 |
Step 2: Take the base a log of both
sides. |
| Step 3: Apply the power rule for logarithms. |
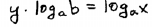 |
|
| |
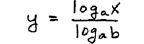 |
Step 4: Solve for y. |
| |
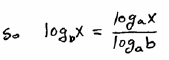 |
For the last step simply equate the
equivalent forms of y above. |
We can also use the one-to-one property for logarithms to
solve logarithmic equations. If we are given an equation with a logarithm of the
same base on both sides we may simply equate the arguments.
Be sure to check to see if the solutions that we obtain
solve the original logarithmic equation. In this manual we will put a check mark
next to the solution after we determine that it really does solve the equation.
This process sometimes results in extraneous solutions so we must check our
answers.
|