Literal Equations & Formula

A literal equation is an equation which consists primarily of letters.
Formulas are an example of literal equations.
Each variable in the equation "literally" represents an important part of the whole relationship
expressed by the equation.

For example,

The perimeter of a rectangle is expressed as P = 2L + 2W

The "L" represents the length of one side of the rectangle. We see "2L" in the formula since there
are two sides in a rectangle.

The "W" represents the measure of the width. There is a "width" at opposite ends of the
rectangle, hence "2W".

Solving Literal Equations

To solve a literal equation means to rewrite the equation so a different variable stands alone on
one side of the equals sign. We have to be told for which variable we want to solve.

For example,

If we were asked to solve the equation P = 2W + 2L for W,
we would get W = ( P - 2L ) / 2

We started with " P = ..." and ended with " W = ... ".
That's what it means to "solve a literal equation."

Method:
1. Identify the variable that you want to have alone.
2. Treat all other letters as if they were numbers.
You can add, subtract, or multiply by a letter.
You can also divide by a variable as long as it is never zero.
3. Use all of the rules of algebra that you learned to solve equations in the past.
You may need to add the opposite of a variable to both sides of an equation.
You might have to multiply both sides by the reciprocal of the variable.
All rules of algebra apply.
4. Get the variable you want by itself on one side of the equation.

Example 1:

Solve 5x + 2y = 7 for "y".

Solution:

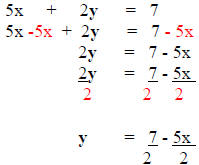	Identify "y" as the variable you want alone.
	Add the opposite of 5x to both sides.
	Divide all terms on both sides by the coefficient of "y"
	Here is your solution.

Rewritten for "y": y = ( 7/2 ) - ( 5/2 )x

Example 2:

Solve T = 2πR(R+h) for h

Solution:

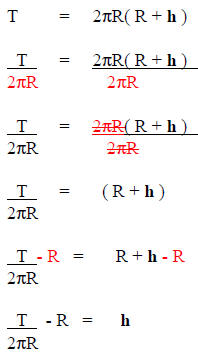	Identify "h" as the variable you want alone.
	Divide both sides by the factors 2πR.
	Cancel.
	To solve for h, add the opposite of R to both sides.
	You are done.

Hence, h = [ T / ( 2πR ) ] - R

If we want to write the answer using a single fraction, we need to express R in terms of the
common denominator 2πR.

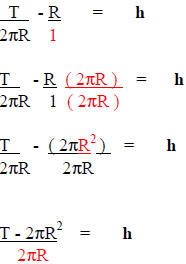	Write R over the denominator of 1
	Multiply the numerator and denominator of R by 2πR.
	Simplify. R times R is R2. We do not use the distributive law since there is no addition inside the parentheses.
	Write answer over the common denominator 2πR.

Rewritten for h, h = ( T - 2πR² ) / ( 2πR )