Systems of Linear Equations
1. For any numbers A,B,C with A and B not both zero at the same time,
the set of points
{(x, y) : Ax + By = C}
is a line. If (x1, y1) and (x2, y2) are two points on this line, then we say
call this set of points the line through (x1, y1) and (x2, y2), and we
have that Ax1 + By1 = C,Ax2 + By2 = C.
2. The equation Ax + By = C is called the equation of a line
3. If a line has equation Ax + by = C with A ≠ 0, then
it intersects the x
axis in exactly one point, which is called the x intercept. Similarly if
B ≠ 0, it intersects the y axis in exactly one point, the
y intercept.
4. The line Ax + by = C has an x intercept if A ≠ 0 and the x intercept
is C/A. The line has a y intercept if B ≠ 0 and the y intercept is C/B.
Another way to do this: To find the x intercept, put y = 0 in the equation
and find the value of x. To find the y intercept, put x = 0 in the equation
and find the value of y.
5. Let Ax+By = C be a line passing through the points (x1, y1) and (x2, y2).
If x1 ≠ x2, then we say that the slope m of the line is
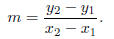
If x2 = x1 and y2 ≠ y1, then the line is vertical and we say that the slope
is not defined. The slope of a line does not depend in which points (x1, y1)
and (x2, y2) we choose.
6. When the slope of a line is m = 0, then the line is horizontal.
7. If B ≠ 0, the slope of the line Ax + By = C is m = −A/B . If B = 0, then
the slope is not defined.
8. Two lines are parallel if they have the same slope, or if the slope is
undefined for both.
9. Another form of the equation of a line is y = mx+b, where m is the slope
and b is the y intercept.
10. The solution of a system of linear equations is their point of
intersection.
11. (i) If two lines have the same slope and their equations are not
multiples of
each other, then they are parallel, so they do not have a common point of
intersection. Therefore the system of equations does not have a solution..
(ii) If two lines have the same slope and their equations are multiples
of each other, then they are the same line, so they have infinitely many
solutions.
12. To solve systems of 2 equations with two unknowns:
(I) Method of elimination: Multiply one of the equations by a multiple
of the other in such a way so that when you add them, one of the unknowns
disappears. Then you can find the other unknown.
(II) Method of substitution: Solve the first equations in terms of one
of the unknowns, and replace that unknown in the second equation.
13. A system of equations that has at least one solution is called
consistent,
and one with no solutions is called inconsistent.
14. Theorem on transforming systems of equations: If a system of equations
is transformed into a new system by any of the following operations
(a) Interchange 2 equations.
(b) Multiply any equation by a nonzero number.
(c) Replace any equation by the sum of that equation and a multiple of
any other equation.
then the set of solutions of the transformed system is the same as the set
of solutions of the original system.
15. A matrix is in reduced form if it has the following properties:
(a) The entry in the first row and first column of the coefficient matrix
is 1, and te first nonzero entry in each row is 1.
(b) If a column of the coefficient matrix contains a leading 1, then all
other entries in that column are 0.
(c) As you move from left to right through the columns of the coefficient
matrix, the leading 1s occur in successive rows. In particular, all
rows with only 0s are at the bottom of the matrix.
In this case, we can find the solutions of the new system easily.
16. Algorithm for solving a system of linear equations:
(a) Form the augmented matrix.
(b) Use row operations to transform the augmented matrix into reduced
form.
(c) Interpret the reduced form to obtain information about the solution
set.
i. If there is a row with zeros to the left of the vertical line and a
nonzero entry to the right, then the system has no solutions.
ii. If the system has n equations in n variables and the reduced form
has a leading 1 in each row, then there is a unique solution.
iii. If a consistent system has n variables and the reduced form has
k, k < n, nonzero rows, then there are infinitely many solutions
in n − k of the variables can be specified arbitrarily.
|