System of Equations
Solve each system of equations by the Elimination Method
| ⅔x + 4y = ¨C4, 5x + 6y = 18 |
9x ¨C 3y = 12, 12x ¨C 4y = 18 |
 |
 |
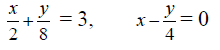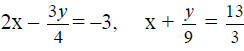Solve each system of equations by the method of your
choice.
| 2x ¨C y = ¨C7, 4x ¨C 3y = ¨C11 |
3x + y = ¨C14, 3y + 4x = ¨C22 |
Write a system of equations and solve.
One number is four more than twice the second number. Their total is 25. Find
the numbers.
Jennifer and Lia purchased 40 stamps, a mixture of 32¢ and
19¢ stamps. Find the number of each type of stamp if they spent $12.15
Write a system of equations and solve.
California 1 South is a historic highway that stretches 123 miles along the
coast from Monterey to Morro Bay. Suppose that two cars start driving this
highway, one from each town. They meet after 3 hours. Find the rate of each car
if one car travels 1 mile per hour faster than the other car.
Find the measures of two complementary angles if one angle
is 10º more than three times the other.
Test 4 Next Thursday, July 16, 2009
For 4 ۰ 5 = 20, the 4 and the 5 are called factors of the
20. Writing 20 as 4 ۰ 5, or as 2 ۰ 10, is writing 20 in factored
form.
Polynomials can also be written in factored form. For
example, a² + 8a + 12 = (a + 6)(a + 2).
The process of writing a polynomial as a product of
factors is called factoring the polynomial.
The greatest common factor (GCF) of a list of
terms is the product of the GCF of the numerical coefficients and the
GCF of the variable factors.
Find the GCF of the following lists of terms.
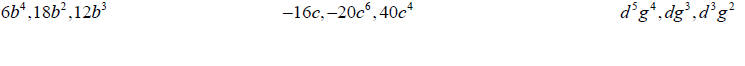
When factoring a polynomial, we consider the GCF of each
term, write it then open parenthesis. We write each
factored term within the parenthesis. For example 2h³ is the GCF of
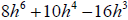 , therefore, to write in factored
form we will fires write the GCF, 2h³, then open parenthesis
2h³(
We will then divide each term of the polynomial by 2h³ and write the quotient in
then close the parenthesis.
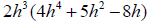 . We can multiply (distribute the 2h³) to
check our result.
Factor the GCF out of the following:
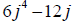
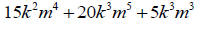
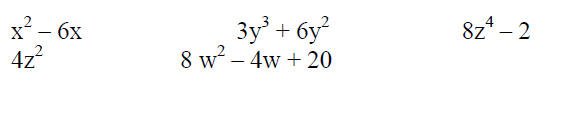
Factor each of the following:
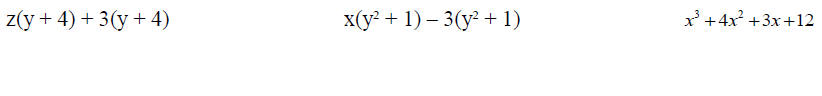
Factor each of the following:
Factor by Grouping:
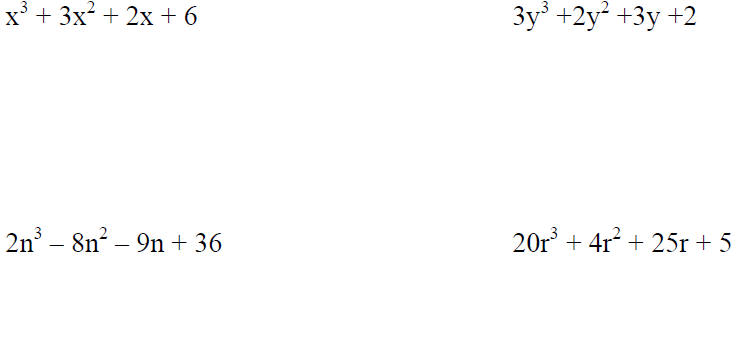
Factoring Trinomials of the form ---- x² + bx + c
Recall from the FOIL Method that
( x + 4 )( x + 3) = x² + 3x + 4x + 12
= x² + 7x + 12
Therefore the factored form of x² + 7x + 12 is ( x + 4 )(
x + 3).
Notice that 4۰3 = 12, the last term, and 4 + 3 = 7, the coefficient of the
middle term.
When we start to factor x² + 7x + 12, we should think of
the factors of 12 that will add to be 7. We know that 1۰12, 2۰6, and 3۰4 all
equal 12, but the pair of 3 & 4 is the only pair that adds to be 7.
If we had x² + 13x + 12 as our trinomial, our factored
form would have been ( x + 1 )( x + 12 ).
If we had x² + 8x + 12 as our trinomial, our factored form would have been ( x +
2 )( x + 6 ).
Keep in mind that due to the commutative property of
multiplication, ( x + 2 )( x + 6 ) = ( x + 6 )( x + 2 ), so it does not matter
which factor we write first
We also need to be aware of a possible GCF which may need
to be factored out of the trinomial as our first step of the factoring process.
For example, to factor 20. 3x² + 30x + 63, we will start
by dividing each term by 3.
Factor each of the trinomials completely. If a trinomial
cannot be factored, write prime.
|
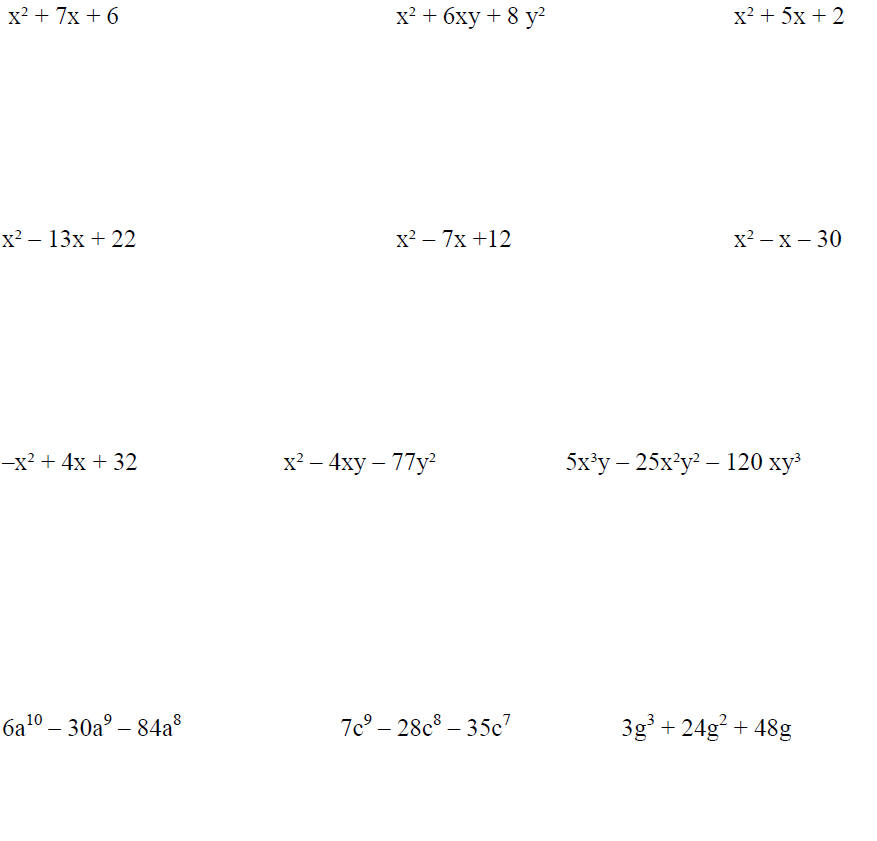
