Solving Quadratic Equations

In this lesson, we’ll look at a different type of equations – quadratic equations. These are
equations of the form ax² + bx + c = 0 and you can solve them either by factoring or by
using the quadratic formula. Then we’ll look at graphs of equations of the form
y = ax² + bx + c .

The first method for solving quadratic equations is factoring. This method makes use of
the Zero Product Property, that is, if ab = 0 , then either a = 0 or b = 0.

The equation must be written in the form ax² + bx + c = 0 , so you may have to rewrite the
equation in this form before you get started. Next you’ll factor the left hand side of the
equation. Once in factored form, you’ll use the Zero Product Property to solve the
equation.

Example 1: Solve for x: x² - 5x -14 = 0

Example 2: Solve for x: x(x - 4) = 12

Example 3: Solve for x: 3x² -17x +10 = 0

Example 4: Solve for x: 25x² - 81 = 0

Sometimes you’ll want to look for a common factor before proceeding as we did on the
first four examples.

Example 5: Solve for x: x² +12x = 0

Example 6: Solve for x: - 6x² -12x + 48 = 0

Another method for solving quadratic equations is the quadratic formula. Here’s the
formula. You need to memorize it:

For a quadratic equation ax² + bx + c = 0 , a ≠ 0 , 

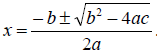
Example 7: Use the quadratic formula to solve: 2x² - 5x -1 = 0 .

Example 8: Use the quadratic formula to solve: x² +10x + 6 = 0 .

Example 9: Use the quadratic formula to solve: 5x² - 2x = 3 .

Note: you can use the quadratic formula to solve ALL quadratic equations. Factoring
may be an easier method to use.

Next we’ll look at graphs of equations of the form y = ax² + bx + c . The graph of this
equation is called a parabola. To graph these equations, you will need to find four pieces
of information about the graph:

1. The direction the parabola opens – up or down. This will be determined by the
leading coefficient. If the leading coefficient is positive, your parabola will open
upwards. If the leading coefficient is negative, it will open downwards.

2. The y intercept. To find the y intercept, you’ll let x = 0 and find y.

3. The x intercept(s). To find the x intercept(s), you let y = 0 and solve for x.

4. The location of the vertex, the high point or the low point of the graph. To find the x
value of the vertex, use the formula 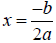. To find the y value of the vertex, you’ll
substitute the x value you found into the equation and evaluate.

Example 10: State whether the parabola opens upwards or downwards and find the x and
y intercepts and the vertex. Then graph the equation.

y = x² - 4x + 3

Example 11: State whether the parabola opens upwards or downwards and find the x and
y intercepts and the vertex. Then graph the equation.

y = x² + 2x +1

Example 12: State whether the parabola opens upwards or downwards and find the x and
y intercepts and the vertex. Then graph the equation.

y = 3x² - 2x -1

Example 13: State whether the parabola opens upwards or downwards and find the x and
y intercepts and the vertex. Then graph the equation.

y = x² - 2x - 4

You can use quadratic equations to solve some problems. For the last example, write a
quadratic equation and use it to solve the problem

Example 14: A customer wants to surround her swimming pool with a paved walkway.
The pool measures 30 feet by 40 feet, and she wants to use 296 square feet of paving
material. How wide can the walkway be?