DISTANCE,CIRCLES,AND QUADRATIC EQUATIONS

• DISTANCE BETWEEN TWO POINTS IN THE PLANE
Suppose that we are interested in finding the distance d between two points P₁(x₁, y₁) and
P₂(x₂, y₂) in the xy-plane. If, as in Figure G.1, we form a right triangle with P₁ and P₂
as vertices, then it follows from Theorem B.4 in Appendix B that the sides of that triangle
have lengths |x₂ − x₁| and |y₂ − y₁|. Thus, it follows from the Theorem of Pythagoras that

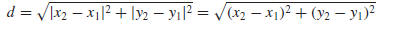
and hence we have the following result.

G.1 theorem. The distance d between two points P₁(x₁, y₁) and P₂(x₂, y₂) in a
coordinate plane is given by

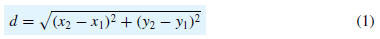
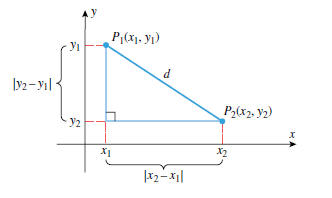
Figure G.1

To apply Formula (1) the scales on the coordinate axes must be the same; otherwise, we would not
have been able to use the Theorem of Pythagoras in the derivation. Moreover, when using Formula
(1) it does not matter which point is labeled P₁ and which one is labeled P₂, since reversing the
points changes the signs of x₂ − x₁ and y₂ − y₁; this has no effect on the value of d because these
quantities are squared in the formula. When it is important to emphasize the points, the distance
between P₁ and P₂ is denoted by d(P₁, P₂) or d(P₂, P₁).

Example 1 Find the distance between the points (−2, 3) and (1, 7).

Solution. If we let (x₁, y₁) be (−2, 3) and let (x₂, y₂) be (1, 7), then (1) yields

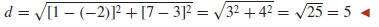
Example 2 It can be shown that the converse of the Theorem of Pythagoras is true;
that is, if the sides of a triangle satisfy the relationship a² + b² = c², then the triangle must
be a right triangle. Use this result to show that the points A(4, 6), B(1,−3), and C(7, 5)
are vertices of a right triangle.

Solution. The points and the triangle are shown in Figure G.2. From (1), the lengths of the sides of the triangles are

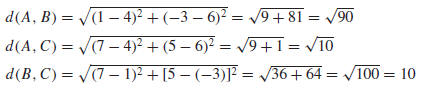
Since

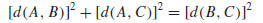
it follows that ABC is a right triangle with hypotenuse BC.

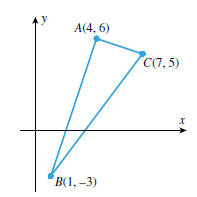
Figure G.2

• THE MIDPOINT FORMULA
It is often necessary to find the coordinates of the midpoint of a line segment joining two
points in the plane. To derive the midpoint formula, we will start with two points on a coordinate
line. If we assume that the points have coordinates a and b and that a ≤ b, then,
as shown in Figure G.3, the distance between a and b is b − a, and the coordinate of the
midpoint between a and b is

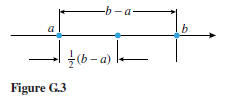
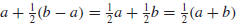
which is the arithmetic average of a and b. Had the points been labeled with b ≤ a, the
same formula would have resulted (verify). Therefore, the midpoint of two points on a
coordinate line is the arithmetic average of their coordinates, regardless of their relative
positions.

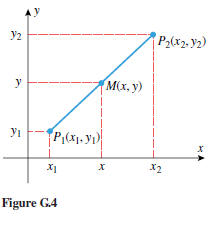
If we now let P₁(x₁, y₁) and P₂(x₂, y₂) be any two points in the plane and M(x, y) the
midpoint of the line segment joining them (Figure G.4), then it can be shown using similar
triangles that x is the midpoint of x₁ and x₂ on the x-axis and y is the midpoint of y₁ and y₂
on the y-axis, so

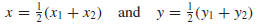
Thus, we have the following result.

G.2 theorem (The Midpoint Formula). The midpoint of the line segment joining
two points (x₁, y₁) and (x₂, y₂) in a coordinate plane is

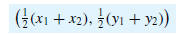
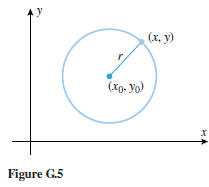
Example 3 Find the midpoint of the line segment joining (3,−4) and (7, 2).

Solution. From (2) the midpoint is

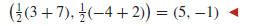
• CIRCLES
If (x₀, y₀) is a fixed point in the plane, then the circle of radius r centered at (x₀, y₀) is the
set of all points in the plane whose distance from (x₀, y₀) is r (Figure G.5). Thus, a point

(x, y) will lie on this circle if and only if

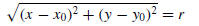
or equivalently,

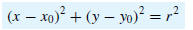
This is called the standard form of the equation of a circle.

Example 4 Find an equation for the circle of radius 4 centered at (−5, 3).

Solution. From (3) with x₀ = −5, y₀ = 3, and r = 4 we obtain

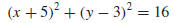
If desired, this equation can be written in an expanded form by squaring the terms and then
simplifying:

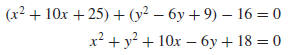
Example 5 Find an equation for the circle with center (1,−2) that passes through
(4, 2).

Solution. The radius r of the circle is the distance between (4, 2) and (1,−2), so

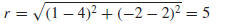
We now know the center and radius, so we can use (3) to obtain the equation

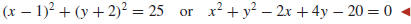
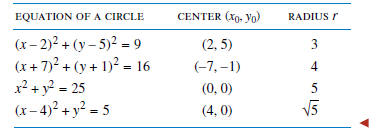
FINDING THE CENTER AND RADIUS OF A CIRCLE
When you encounter an equation of form (3), you will know immediately that its graph is a
circle; its center and radius can then be found from the constants that appear in the equation:

Example 6

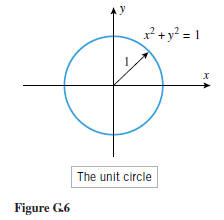
The circle x² + y² = 1, which is centered at the origin and has radius 1, is of special
importance; it is called the unit circle (Figure G.6).

OTHER FORMS FOR THE EQUATION OF A CIRCLE
Analternative version of Equation (3) can be obtained by squaring the terms and simplifying.
This yields an equation of the form

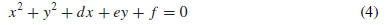
where d, e, and f are constants. (See the final equations in Examples 4 and 5.)

Still another version of the equation of a circle can be obtained by multiplying both sides
of (4) by a nonzero constant A. This yields an equation of the form

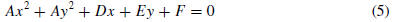
where A, D, E, and F are constants and A ≠ 0.
If the equation of a circle is given by (4) or (5), then the center and radius can be found by
first rewriting the equation in standard form, then reading off the center and radius from that
equation. The following example shows how to do this using the technique of completing
the square. In preparation for the example, recall that completing the square is a method
for rewriting an expression of the form

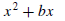
as a difference of two squares. The procedure is to take half the coefficient of x, square it,
and then add and subtract that result from the original expression to obtain

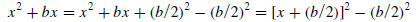
Example 7 Find the center and radius of the circle with equation

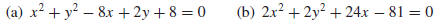
Solution (a). First, group the x-terms, group the y-terms, and take the constant to the
right side:

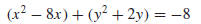
Next we want to add the appropriate constant within each set of parentheses to complete the
square, and subtract the same constant outside the parentheses to maintain equality. The
appropriate constant is obtained by taking half the coefficient of the first-degree term and
squaring it. This yields

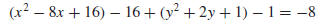
from which we obtain

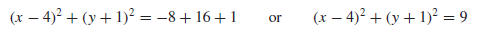
Thus from (3), the circle has center (4,−1) and radius 3.

Solution (b). The given equation is of form (5) with A = 2. We will first divide through
by 2 (the coefficient of the squared terms) to reduce the equation to form (4). Then we will
proceed as in part (a) of this example. The computations are as follows:

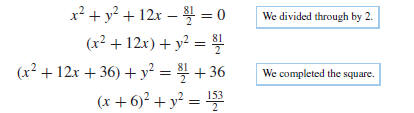
From (3), the circle has center (−6, 0) and radius

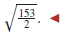
• DEGENERATE CASES OF A CIRCLE
There is no guarantee that an equation of form (5) represents a circle. For example, suppose
that we divide both sides of (5) by A, then complete the squares to obtain

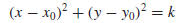
Depending on the value of k, the following situations occur:

• (k > 0) The graph is a circle with center (x₀, y₀) and radius
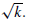
• (k = 0) The only solution of the equation is x = x₀, y = y₀, so the graph is the single
point (x₀, y₀).
• (k < 0) The equation has no real solutions and consequently no graph.

Example 8 Describe the graphs of

Solution (a). There are no real values of x and y that will make the left side of the
equation negative. Thus, the solution set of the equation is empty, and the equation has no
graph.

Solution (b). The only values of x and y that will make the left side of the equation 0
are x = 1, y = −4. Thus, the graph of the equation is the single point (1,−4).

The following theorem summarizes our observations.

The last two cases in Theorem G.3 are
called degenerate cases. In spite of
the fact that these degenerate cases
can occur, (6) is often called the
general equation of a circle.

G.3 theorem. An equation of the form

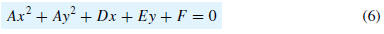
where A ≠ 0, represents a circle, or a point, or else has no graph.