Rational Expressions
Simplifying Rational Expressions (Reducing to Lowest Term)
•Factor both the numerator and denominator relative to the integers. Hint: Try
to find the
greatest common factor first!
•Reduce factors common to both the numerator and denominator.
Adding and Subtracting Rational Expressions
•Factor the numerator and denominator relative to the
integers.
•Cross-cancel as much as possible.
•Find the Least Common Denominator (LCD) by factoring each denominator into
prime
factors and forming a product of all distinct prime factors. Use the factor to
highest power if
two or more factors are not distinct.
•Change each fraction to an equivalent fraction using the LCD.
•Add or subtract numerators keeping the same denominator.
•Reduce, if possible.
The Least Common Denominator (LCD) is the smallest
number that is
evenly divisible (no remainder) by each of the denominators of the fractions
being added. If the denominators are all prime numbers, the LCD is the
product of the denominators. If one or more of the denominators is NOT a
prime number, the LCD is a product using the largest listing of of each prime
number taking into account ALL denominators.
the LCD is the product found by using certain prime number
factors of each
denominator.
A prime number is a whole number other than 0 and
1 that is divisible only by
itself and 1. For example, 2, 3, 5, 7, 11, 13, 17, etc. are prime
numbers. In
the case of polynomial expressions, they are called "prime" if they cannot be
factored relative to the integers.
Multiplying and Dividing Rational Expressions
Multiplying and Dividing Rational Expressions
•Factor the numerator and denominator relative to the
integers.
•Cross-cancel as much as possible.
•Multiply the numerators AND multiply the denominators.
Division Rule:
•Convert the division to an equivalent multiplication
problem using the reciprocal ** of the
divisor as the multiplier.
•Then multiply according to the rule for multiplying rational expressions.
** Interchanging the numerator and denominator of a
fraction results in a fraction that is
called the reciprocal of the original fraction. When a number is multiplied by
its
reciprocal, the product equals 1.
Finding Solutions of Rational Equations
•Find the Least Common Denominator (LCD).
•Multiply both sides of the equation by the LCD, reduce, and solve.
•Check the solutions in the original equation, rejecting any that produce 0
or an imaginary
number in the denominator.
Problem 1:
Simplify
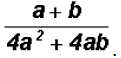
Please note that you are asked to "simplify". This
means that you have
to reduce the rational expression to lowest term.
The numerator cannot be factored relative to the integers.
Let's factor out the greatest
common factor in the denominator.
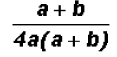
Since we know that
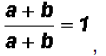
we can further reduce to get
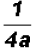 , which is the final reduced form. , which is the final reduced form.
Problem 2:
Simplify
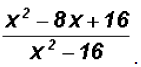
Let's factor the numerator and denominator relative to the
integers
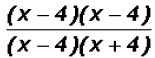
Since we know that
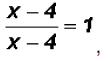
we can further reduce to get
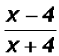 , which is the final reduced form. , which is the final reduced form.
Problem 3:
Simplify
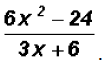
Let's factor out the greatest common factor in the
numerator and the denominator.
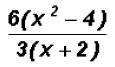
Now, we know that 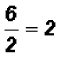 and
we can also further factor the denominator to get and
we can also further factor the denominator to get
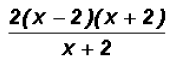
Since we know that 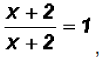
we can further reduce to get
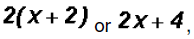 which is the final reduced form. which is the final reduced form.
Problem 4:
Simplify 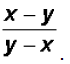
This is somewhat "tricky." Notice that we have an x
and a y in the numerator and the
denominator. But their signs are opposite.
Whenever this happens, simply factor a -1 out of
the numerator OR the denominator.
Let's see what happens if we factor a -1 out of the
denominator:
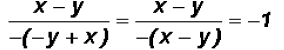
We found the final reduced form to be a constant, namely
the number -1.
Problem 5:
Simplify 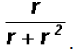
The numerator cannot be factored relative to the integers.
Let's factor out the greatest
common factor in the denominator.
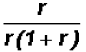
Since we know that 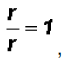
we can further reduce to get
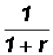 , which is the final reduced form. , which is the final reduced form.
Problem 6:
Simplify
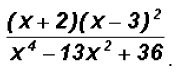
Let's factor the numerator and denominator. Please note
that we have a polynomial
expression in the denominator that behaves "like a quadratic"!
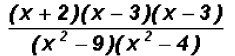
We also notice that the two factors in the denominator are
Differences of Squares which
can be factored as follows:
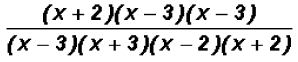
we can now reduce to get
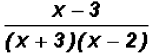 , which can also be written as , which can also be written as
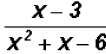
Problem 7:
Add
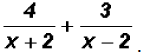
The numerators and denominators cannot be factored
relative to the integers.
Let's find the Least Common Denominator.
Since both denominators are prime, the LCD is the product
found by
multiplying both denominators.
Therefore, the LCD is 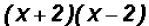 !!!
!!!
Next, we change each fraction to an equivalent fraction
using the LCD.
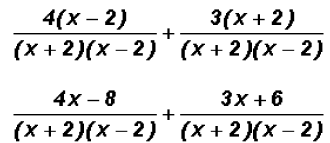
then we add the numerators keeping the same denominator
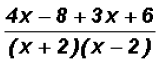
and the final sum is 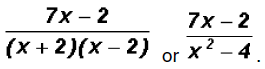
Problem 8:
Subtract 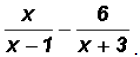
The numerators and denominators cannot be factored
relative to the integers.
Let's find the Least Common Denominator.
Since both denominators are prime, the LCD is the product found by
multiplying both denominators.
Therefore, the LCD is 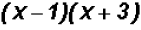 !!!
!!!
Next, we change each fraction to an equivalent fraction
using the LCD.
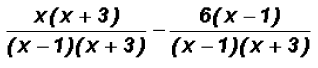
and 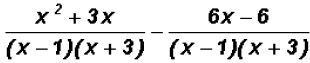 Please note that
the minus sign is in front of Please note that
the minus sign is in front of
the ENTIRE numerator 6x - 6 !
Therefore, we have to keep the minus sign is in front of
the ENTIRE numerator as follows:
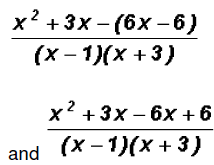
The final sum is 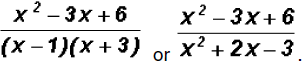
Problem 9:
Subtract
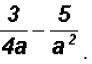
The numerators cannot be factored relative to the
integers.
Let's find find the Least Common Denominator.
Factor all denominators into prime factors as follows:
4a: This expression is not "prime" because we can factor
it as 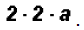
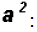 This expression is not
"prime" because can factor it as This expression is not
"prime" because can factor it as 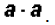
Since the denominators are NOT prime, the LCD is the
product found by
creating a product using the largest listing of of each prime expression taking
into account ALL denominators.
In our case, the number 2 is listed twice and the
expression a is listed twice.
Therefore, the LCD is 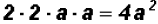 !!! !!!
Next, we change each fraction to an equivalent fraction
using the LCD.
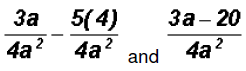
Problem 10:
Add
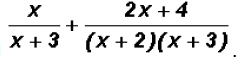
One numerator can be factored relative to the integers,
but the denominators are already
factored.
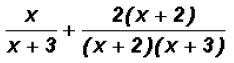
Now we can reduce the second term as follows:
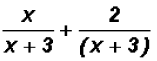
and we can immediately state the sum to be
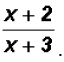
Problem 11:
Subtract 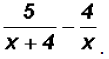
The numerators and denominators cannot be factored
relative to the integers.
Let's find the Least Common Denominator.
Since both denominators are prime, the LCD is the product found by
multiplying both denominators.
Therefore, the LCD is x(x + 4) !!!
Next, we change each fraction to an equivalent fraction using the LCD.
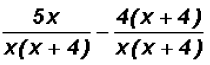
and 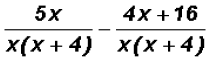 Please note that
the minus sign is in front of the ENTIRE Please note that
the minus sign is in front of the ENTIRE
numerator 4x + 16 !
Therefore, we have to keep the minus sign is in front of
the ENTIRE numerator as follows:
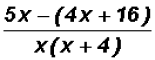
and 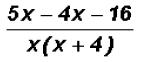
The final sum is 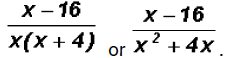
Problem 12:
Multiply 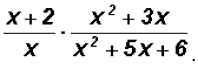
First we are going to factor the numerators and the
denominators.
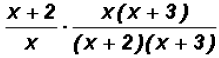
Next we will cross-cancel as follows:
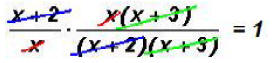
Problem 13:
Divide 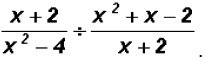
First we are going to factor the numerators and the
denominators.
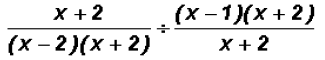
Next we will cross-cancel within each term to get:
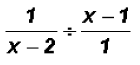
Then, we convert the division to an equivalent
multiplication problem using the reciprocal
of the divisor as the multiplier.
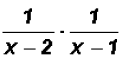
and we get 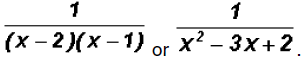
Problem 14:
Write the compound fraction
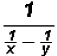 as a simple fraction. as a simple fraction.
In this case, we first find the Least Common Denominator
taking into account
all of the denominators. In our case, x and y.
Since both denominators are prime, the LCD is the product found by
multiplying both denominators.
Therefore, the LCD is xy !!!
Then, we multiply both the numerator and denominator of
the compound fraction by the
LCD.
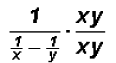
Next, we must distribute the numerator of the LCD to the
numerator of the compound
fraction and, furthermore, we must distribute the denominator of the LCD to ALL
terms of
the denominator of the compound fraction.
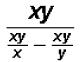
finally we reduce in the denominator to get the simple
fraction 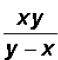 . .
Problem 15:
Solve 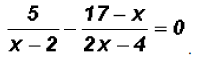
First, we find the Least Common Denominator.
Factor all denominators into prime factors as follows:
x - 2: This expression is called "prime" because it is not
factorable relative to the integers.
2x - 4: This expression is not "prime" because we can
factor out a
2 and write 2(x - 2).
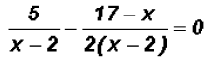
Since one denominator is NOT prime, the LCD is the product
found by
creating a product using the largest listing of of each prime expression taking
into account ALL denominators.
In our case, the number 2 is listed once and the
expression x - 2 is listed
once. Therefore, the LCD is 2(x - 2) !!!
Next, we multiply both sides of the equation by the LCD
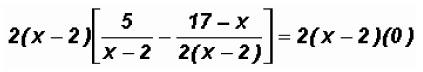
then we distribute the LCD to ALL terms on each side
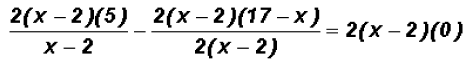
Please note that 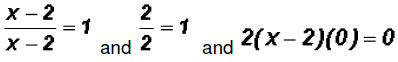 !!!!!!!!!!!!!!!!!!!!!! !!!!!!!!!!!!!!!!!!!!!!
!!!
and finally we reduce each term and solve
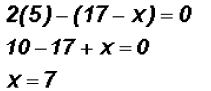
Any time we solve a rational equation we MUST check
the solutions in the original
equation, rejecting any that produce 0 or an imaginary number in the
denominator.
In our case, we must replace the variable with 7 in the
original equation to make sure that
the value to the left of the equal sign becomes equal to the one on the right,
which is 0.
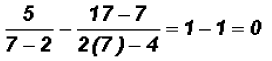
Since the value of the left side equals 0, which is
also the value of the right side, we
can say that the solution is indeed 7.
Problem 16:
Solve 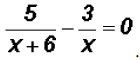
First, we find the Least Common Denominator.
Factor all denominators into prime factors as follows:
x + 6: This expression is called "prime" because it is not
factorable relative to the integers.
x: This expression is called "prime" because it is not factorable
relative to the integers.
Since both expressions are prime, the LCD is found by multiplying them.
Therefore, the LCD is x(x + 6) !!!
Multiplying both sides by the LCD we get
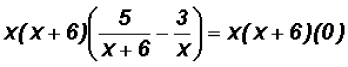
then we distribute the LCD to ALL terms on each side
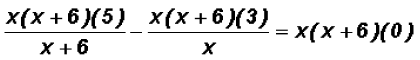
Please note that 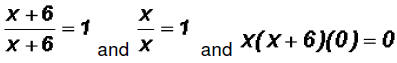 !!!!!!!!!!!!!!!!!!!!!! !!!!!!!!!!!!!!!!!!!!!!
!!!
and finally we reduce each term and solve
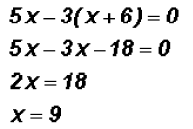
Again, we must check the solutions in the original
equation, rejecting any that produce 0
or an imaginary number in the denominator.
In this case, we must replace the variable with 9 in the
original equation to make sure that
the value to the left of the equal sign becomes equal to the one on the right,
which is 0.
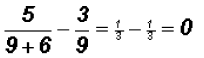
Since the value of the left side equals 0, which is
also the value of the right side, we
can say that the solution is indeed 9.
Problem 17:
Solve 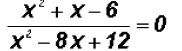
Since we only have one rational expression, we simply
multiplying both sides by the
denominator
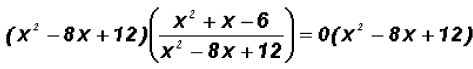
and when we multiply the left side, we get
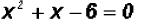
Please note that 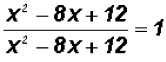 !!!!!!!!!!!!!!!!!!!!!!!!!
!!!!!!!!!!!!!!!!!!!!!!!!!
and then we reduce to get
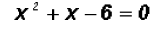
The trinomial on the right can be factored as follows
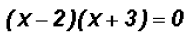
and then we can use the Zero Product Principle to find the
solutions
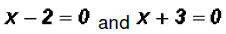
so that 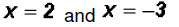
Again we must check the solutions in the original
equation, rejecting any that produce 0
or an imaginary number in the denominator.
First, we must replace the variable with -3 in the
original equation to make sure that the
value to the left of the equal sign becomes equal to the one on the right, which
is 0.
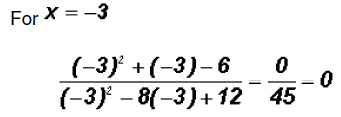
Since the value of the left side equals 0, which is
also the value of the right side, we
can say that the solution is indeed -3.
Next, we must replace the variable with 2 in the original
equation to make sure that the
value to the left of the equal sign becomes equal to the one on the right, which
is 0.
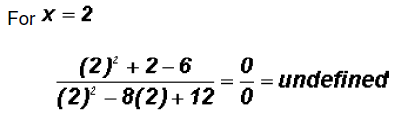
Since the value of the left side is undefined, we can
say that 2 is NOT a solution.
Note that any time a 0 appears in the denominator the
expression becomes undefined !
We find that this rational equation only has ONE
solution, namely -3.
Problem 18:
Solve
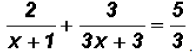
First, we find the Least Common Denominator.
Factor all denominators into prime factors as follows:
3: This number is "prime".
x + 1: This expression is called "prime" because it is not
factorable relative to the integers.
3x + 3: This expression is not "prime" because we can factor out
a 3 and write 3(x + 3).
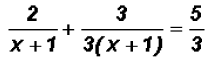
Since one denominator is NOT prime, the LCD is the product
found by
creating a product using the largest listing of of each prime expression taking
into account ALL denominators.
In our case, the number 3 is listed once and the
expression x + 1 is listed
once. Therefore, the LCD is 3(x + 1) !!!
Next, we multiply both sides of the equation by the LCD
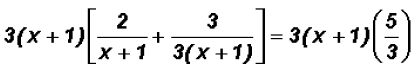
then we distribute the LCD to ALL terms on each side and
reduce
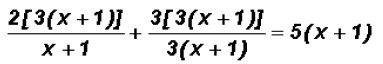
and 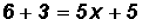
and finally we reduce each term and solve
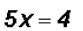
and 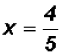
Any time we solve a rational equation we MUST check the
solutions in the original
equation, rejecting any that produce 0 or an imaginary number in the
denominator.
In our case, we must replace the variable with
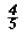 in the original equation to make sure that in the original equation to make sure that
the value to the left of the equal sign becomes equal to the one on the right,
which is 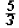
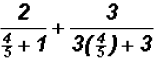
and adding in the denominators, we get
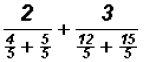
this results in the following complex fraction
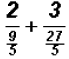 , which can be simplified as follows: , which can be simplified as follows:
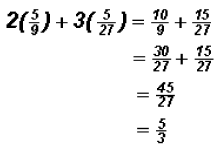
Since the value of the left side equals
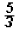 , which is also the value of the right side,
we , which is also the value of the right side,
we
can say that the solution is indeed 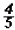 . .
|