Radicals and Rational Exponents
 Evaluate and perform U operations with higher roots.
Evaluate and perform U operations with higher roots.
study Tip
Some higher even and odd roots
occur so frequently that you
might want to memorize them.
Cube Roots
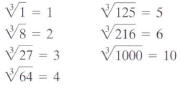
Fourth
Roots
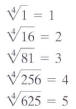
Fifth
Roots
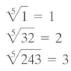
 Rationalize the denominator:
Rationalize the denominator: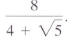
Other Kinds of Roots
We define the principal nth root of a real number a, symbolized by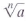 ,
as follows: ,
as follows:
Definition of the Principal nth Root of a Real Number
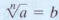 means that b^n = a.
means that b^n = a.
If n, the index is even, then a is nonnegative (a ≥ 0) and b is also
nonnegative
(b ≥ 0). If n is odd, a and b can be any real numbers.
For example,
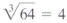 because 43 = 64 and
because 43 = 64 and
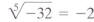 because (-2)5 = -32.
because (-2)5 = -32.
The same vocabulary that we learned for square roots
applies to nth roots. The
symbol
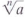 is called a radical and a is called the radicand.
is called a radical and a is called the radicand.
A number that is the nth power of a rational number is
called a perfect nth
power. For example, 8 is a perfect third power, or perfect cube, because
8 = 23. Thus,
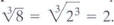 In general, one of the following rules can be used to find nth roots
In general, one of the following rules can be used to find nth roots
of perfect nth powers:
Finding nth Roots of Perfect nth Powers
If n is odd,
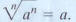
If n is even,
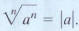
For example,

Absolute value is not needed with odd
roofs, but is necessary with even roofs.
The Product and Quotient Rules for Other Roots
The product and quotient rule apply to cube roots, fourth roots, and all
higher roots.
The Product and Quotient Rules for nth Roots
For all real number, where the indicated roots represent real numbers,
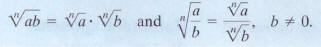
EXAMPLE· 8 Simplifying, Multiplying, and Dividing Higher
Roots
Simplify:
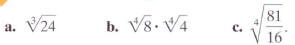
Solution
 Understand
and use rational exponents. Understand
and use rational exponents.
 Simplify:
Simplify:
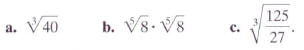
We have seen that adding and subtracting square roots
often involves simplifying
terms. The same idea applies to adding and subtracting nth roots.
EXAMPLE 9 Combining Cube Roots
Subtract: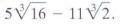
Solution
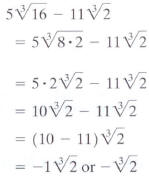 |
Factor 16. 8 is the greatest perfect cube factor:
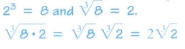
Multiply: 5·2 = 10.
Applythe distributive property.
Simplify. |
 Subtract: Subtract: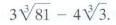
Rational Exponents
We define rational exponents so that their properties are the same as the
properties
for integer exponents. For example, we know that exponents are multiplied when
an
exponential expression is raised to a power. For this to be true,
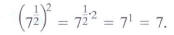
We also know that
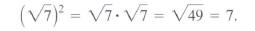
Can you see that the square of both
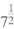 and
and
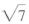 is 7? It is reasonable to conclude
is 7? It is reasonable to conclude
that
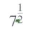 means means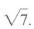
We can generalize the fact that
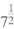 means
means
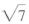 with the following definition:
with the following definition:
EXAMPLE 10 Using the Definition of
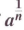
Simplify:
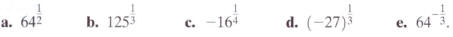
Solution
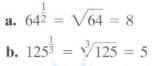
The denominator is the index.
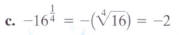
The base is 16 and the negative sign is not affected by the exponent.
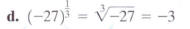
Parentheses show that the base is -27 and that the negative sign is affected by
the exponent.
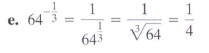
 Simplify:
Simplify:
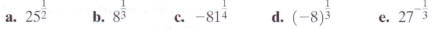
In Example 10 and Check Point 10 each rational exponent
had a numerator of
1. If the numerator is some other integer, we till want to multiply exponent
when
raising a power to a power. For this reason,
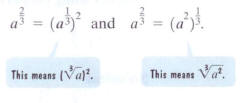
Thus,
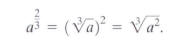
Do you see that the denominator, 3, of the rational
exponent is the same as the
index of the radical? The numerator, 2, of the rational exponent serves as an
exponent in each of the two radical forms. We generalize these ideas with the
following
definition:
The Definition of
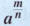
If
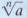 represents a real number and m/n is a positive rational number, n≥2, then
represents a real number and m/n is a positive rational number, n≥2, then
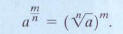
Also,
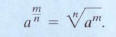
Furthermore, if
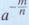 is a nonzero real number, then
is a nonzero real number, then
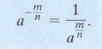
The first form of the definition of
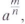 shown again below, involves taking the root
shown again below, involves taking the root
first. This form is often preferable because smaller numbers are involved.
Notice that
the rational exponent consists of two parts, indicated by the following voice
balloons:
The numerator is the exponent.

EXAMPLE 11 Using the Definition of
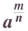
Simplify:
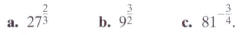
Solution
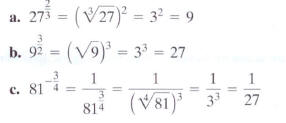
Technology
Here are the calculator keystroke
sequences for
Many Scientific Calculators

Many Graphing Calculators

 Simplify: Simplify:
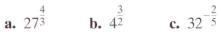
Properties of exponents can be applied to expressions
containing rational
exponents.
EXAMPLE 12 Simplifying Expressions with Rational
Exponents
Simplify using properties of exponents:
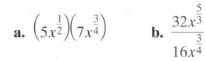
Solution
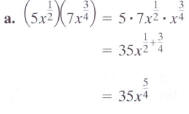 |
Group factors with the same base.
When multiplying expressions with the same base, add
the exponents.
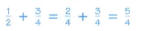 |
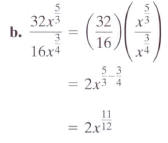 |
Group factors with the same base.
When dividing expressions with the same base, subtract the
exponents.
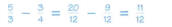 |
 Simplify: a
Simplify: a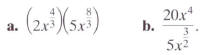
Rational exponents are sometimes useful for simplifying radicals by reducing
their index.
EXAMPLE 13 Reducing the Index of a Radical
Simplify: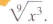
Solution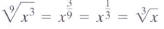
 Simplify: Simplify: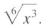
EXERCISE SET P.3
Practice Exercises
Evaluate each expression in Exercises 1-12, or indicate
that the root is not a real number.
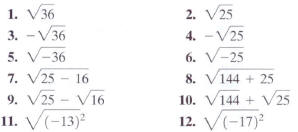
Use the product rule to simplify the expressions in
Exercises
13-22. In Exercises 17-22, assume that variable represent nonnegative
real numbers.

Use the quotient rule to simplify the expressions in
Exercises
23-32. Assume that x > 0.


In Exercises 33-44, add or subtract terms whenever possible.

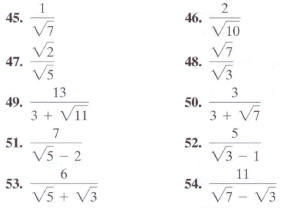
In Exercises 45-54, rationalize the denominator.
Evaluate each expression in Exercises 55--66, or indicate
that the
root is not a real number.


Simplify (he radical expressions in Exercises 67-74.

In Exercises 75-82, add or subtract terms whenever
possible.

In Exercises 83-90, evaluate each expression without using
a
calculator.
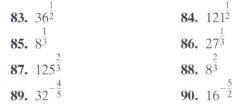
In Exercises 91-100, simplify using properties of
exponents.
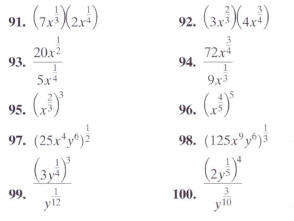
1n Exercises 101-108, simplify by reducing (he index of
the radical.

Practice Plus
In Exercises 109-110, evaluate each expression.
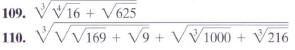
In Exercises 111-114, simplify each expression. Assume
that all
variables represent positive numbers.
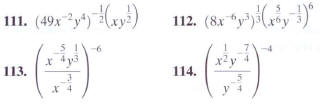
Application Exercises
The formula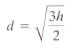
models the distance, d, in miles, that a person h feet
high can see to
the horizon. Use this formula to solve Exercises 115- 116.
115. The pool deck on a cruise ship is 72 feet above the
water.
How far can passengers on the pool deck see? Write the
answer in simplified radical form. Then use the simplified
radical form and a calculator to express the answer to the
nearest tenth of a mile.
116. The captain of a cruise ship is on the star deck,
which is 120
feet above the water. How far can the captain see? Write
the answer in simplified radical form. Then u e the simplified
radical form and a calculator to express the answer to
the nearest tenth of a mile.
Police use the formula
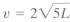 to estimate the speed of a car, v,
to estimate the speed of a car, v,
in miles per hour, based on the length, L, in feet, of its skid marks
upon sudden braking on a dry asphalt road. Use the formula to
solve Exercises 117-118.
117. A motorist is involved in an accident. A police
officer measures
the car's skid marks to be 245 feet long. Estimate the
peed at which the motorist was traveling before braking. If
the posted speed limit is 50 miles per hour and the motorist
tells the officer he was not speeding, should the officer
believe him? Explain.
118. A motorist is involved in an accident. A police
officer measures
the car's skid marks to be 45 feet long. Estimate the
speed at which the motorist was traveling before braking. If
the posted speed limit is 35 miles per hour and the motorist
tells the officer she was not speeding, should the officer
believe her? Explain.
119.In the Peanuts cartoon shown below, Woodstock appears
to
be working step mentally. Fill in the mi sing steps that show
how to go from
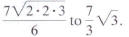

PEA NUTS reprinted by permission of United Feature
Syndicate, Inc.
|