Solving Equations & Inequalities
Solutions to Examples
7.1.
(a) Solve for x: 4x+5 = 0
Solution:
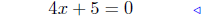 |
given |
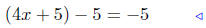 |
subtract −5 from both sides |
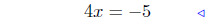 |
combine |
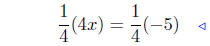 |
multi. both sides by 1/4 |
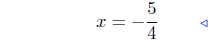 |
combine and done! |
Solving an equation consists of a sequence of legal steps: adding
the same quantity to both sides (see equation (1)); multiplying
both sides by the same quantity (see equation (2)) were used
above.
Presentation of Answer: 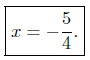
(b) Solve for x: 1/2x − 4 = 6.
Solution:
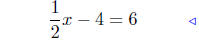 |
given |
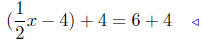 |
add 4 to both sides |
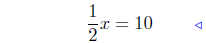 |
combine |
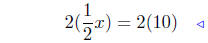 |
multi. both sides by 2 |
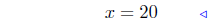 |
combine and done! |
Note this equation initially was not of the form ax + b = 0.
There was a nonzero constant on right-hand side of the equation.
Obviously, the equation (1/2)x−4 = 6 is equivalent to (1/2)x−10 = 0;
consequently, no big deal was made of it.
Presentation of Solution: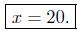
(c) Solve for x: 7 − 3x = 2.
Solution:
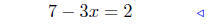 |
given |
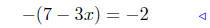 |
multiply both sides by −1 |
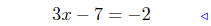 |
simplify |
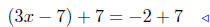 |
add 7 to both sides |
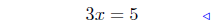 |
combine |
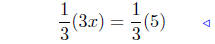 |
multiply both sides by 1/3 |
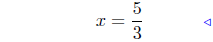 |
combine and done! |
Comments: Here the coefficient of x was negative. I opted to
multiplyb y −1 to ‘change the sign’ so that I would feel more
comfortable solving.
Presentation of Answer: 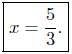
7.2. Solutions:
(a) Solve for x: (x − 1)2 = x2.
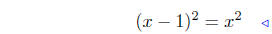 |
given |
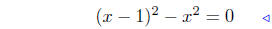 |
sub. x2 both sides: see (1) |
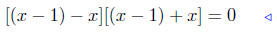 |
diff. of squares! |
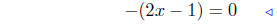 |
combine |
 |
multipy by −1: see (2) |
 |
add 1 to both sides: see (1) |
 |
divide by 2: see (3) |
Comments: Note the recommended way of handling an equation
with squares on both sides. Rather than taking the square root
of both sides, take everything to one side of the equation and
factor it as a difference of squares: this is a much nicer method.
The other option is to expand all binomials and combine.
Presentation of Answer: 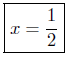
(b) Solve for x: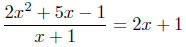
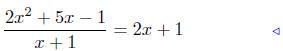 |
given equation |
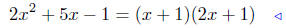 |
multiply both sides by x + 1 |
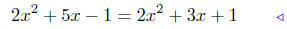 |
expand r.h.s. |
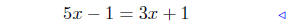 |
sub. 2x2 from both sides: (1) |
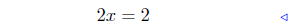 |
two steps in one! |
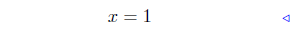 |
divide both sides by 2 |
Presentation of Answer:
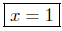
(c) Solve for x: 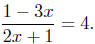
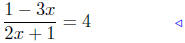 |
given equation |
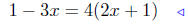 |
multiply both sides by 2x + 1 |
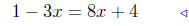 |
expand r.h.s. |
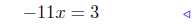 |
add −8x − 1 to both sides |
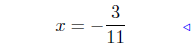 |
divide both sides by 11 |
Presentation of Answer:
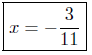
(d) Solve for x: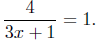
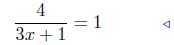 |
the given equation |
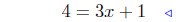 |
multiply both sides by 3x + 1 |
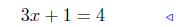 |
transpose equation: a = b <=> b = a |
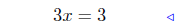 |
add −1 to both sides |
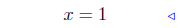 |
divide both sides by 3 |
Presentation of Answer:
7.3. Solutions:
(a) Solve x2 − 5x+6 = 0.
Solution:
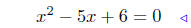 |
given |
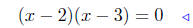 |
factor l.h.s. |
(S-1)
From (S-1) and the Zero-Product Principle, we deduce that
either
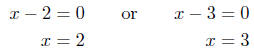
Presentation of Solution:
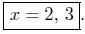
Comments: Note that this equation has two distinct solutions.
An alternate method of presenting the solutions to an
equation is to present the solution set: the set of all solutions.
Here we could have written,
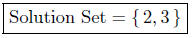
(b) Solve x2 + 4x+4 = 0.
Solution:
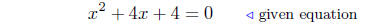
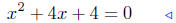 |
given equation |
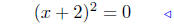 |
factor: perfect square! |
Therefore,
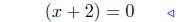 Zero-Product
Principle Zero-Product
Principle
or,
x=-2
Presentation of Answer: 
Comments: The left-hand side is a quadratic polynomial that,
it turned out, was a perfect square. Note that this equation has
only one solution.
(c) Solve 6x2 − x − 2 = 0.
Solution: Let’s take the polynomial aside and factor it using the
factoring techniques explained in Lesson 6.
Factor: 6x2 −x−2 = 0. Begin bytry ing a factorization of the
form
6x2 − x − 2 = (3x + r1)(2x + r2),
where r1 and r2 are chosen so that r1r2 = −2 and the “crossproduct”
is correct. After some trial and error we get r1 = −2
and r2 = 1; thus,
6x2 − x − 2 = (3x − 2)(2x + 1). (S-2)
Solve: Now let’s take the factorization (S-2) and return to our
original equation:
(3x − 2)(2x+1) = 0
We can now obtain the solutions by applying the Zero-Product
Principle: (3x − 2)(2x + 1) = 0 implies either . . .
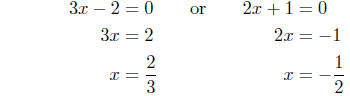
We deduce the solution set is 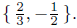
Presentation of Solution: 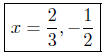
7.4. Solution: This will be short. All the work has been alreadydone.
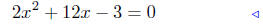 |
given |
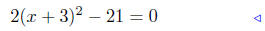 |
complete the square |
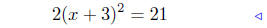 |
equation of the form (7) |
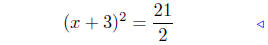 |
divide by 2 |
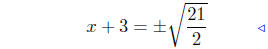 |
take square root |
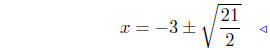 |
solved! |
Presentation of Solution: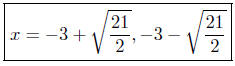
7.5. Solution: Just follow the algorithm.
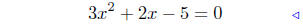 |
given |
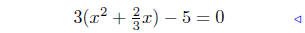 |
Step 2 & 3 |
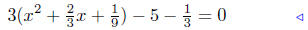 |
Step 4: add/sub 1/2 coeff. of x |
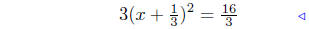 |
perfect square! |
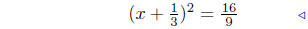 |
divide by 3 |
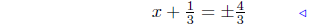 |
take square root both sides |
 |
solve for x and done |
Thus,
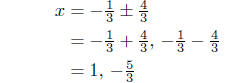
Presentation of Solution: 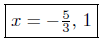
7.6. Solutions: We simply apply the Quadratic Formula!
(a) Solve for x: x2 − 5x + 6 = 0. This is the case where a = 1,
b = −5, and c = 6:
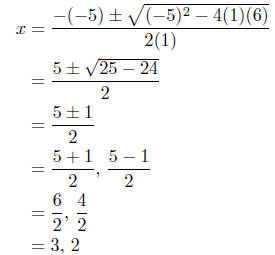
Presentation of Answers: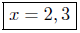
(b) Solve for x: x2+4x+4 = 0. This is the case where a = 1, b = 4,
and c = 4.
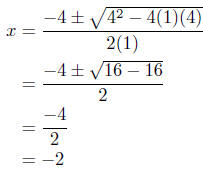
Presentation of Solution: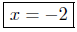
Comments: This is the case of the discriminant of zero. Therefore
we have onlyone solution.
(c) Solve for x: 6x2 − x − 2 = 0. Here a = 6, b = −1, and c = −2.
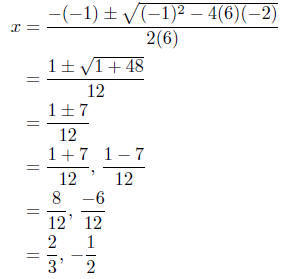
Presentation of Solutions: 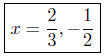
(d) Solve for x: 3x2 − 3x + 1 = 0. This is the case of a = 3, b = −3
and c = 1. Before starting the standard calculations, we might
check the discriminant:
b2 − 4ac = (−3)2 − 4(3)(1) = 9 − 12 = −3 < 0.
We’ve saved ourselves some work. This equation has no solutions.
7.7. Solve 1 + 4y3 ≥ 0. We simply use the tools:
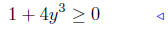 |
given |
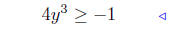 |
add −1 both sides: see (10) |
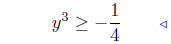 |
multiply 1/4 both sides: see (11) |
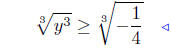 |
by (13) |
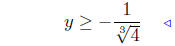 |
apply properties of radicals: see (1) |
The answer can be presented in three ways.
1. Inequalities. Solution: 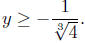
2. Interval Notation. Solution: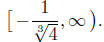
3. Set Notation. Solution: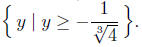
7.8. Solutions:
(a) Solve for x: 5x + 7 < 0.
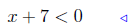 |
given |
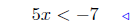 |
add −7 to both sides (10) |
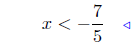 |
multiply both sides by 1/5: see (11) |
Presentation of Answer. Interval Notation: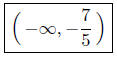
(b) Solve for x: 3 − 9x ≥ 4.
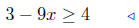 |
given |
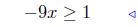 |
add −3 to both sides |
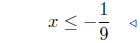 |
mul. by −1/9, inequality reversed! See (12) |
Presentation of Answer. Set Notation: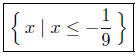
(c) Solve for x: 3x5 + 4 ≥ 9.
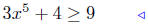 |
given |
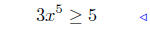 |
add −4 to both sides |
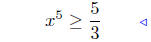 |
multiply by 1/3 |
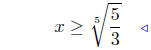 |
take 5th root both sides: See (1) |
Presentation of Answer. Inequalities.
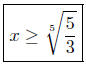
(d) Solve for x: 3x2 + 4 ≤ 3.
 |
given |
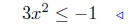 |
add −4 to both sides |
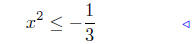 |
divide by 3 |
Now it is apparent that there are no solutions to this equation.
For any x, x2 ≥ 0 so x2 cannot be less than a negative number.
Presentation of Solution. Set Notation. The solution set is
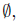
the empty set.
|