Equations and Inequalities with Absolute Value
Def. (1) A relation is a set of ordered
pairs. (2) A relation is a rule of
correspondence between two sets.
EX1. { (Weevil, UAM), (Bulldog, Star City), (Bulldog, LA Tech)}
EX2. To each UAM student record his/her GPA.
Def. (1) A function is a relation in which
no two ordered pairs having the
same first elements have different second elements. (2) A function
is a relation in which to each element in the first set (the domain) there
corresponds exactly one element in the second set (the range).
Question: Is the relation in EX1 a function? Why or why
not?
Question: Is the relation in EX2 a function? Why or why
not?
Activity: Give a specific example of a relation that is
not a function.
Activity: Give a specific example of a relation that is a
function.
Activity: Give a specific example of a function that is
not a relation.
Sometimes a function is represented using functional
notation. The symbol
f(x) is read “f of x” and indicates that the function f is written in terms of
the
variable x. [Note: f(x) does not mean f times x.] f(x) represents the real
number in the range of the function f corresponding to the domain value x.
EX3: If f(x) = 2x2 - x + 3 find
f(2)
f(-3)
f(t)
INTERVAL NOTATION:
SYMBOLIC ALGEBRAIC FORM GRAPH
FORM
[a,b]
(a,b)
[a,b)
[a, ∞)
(a, ∞)
(-∞, a]
(-∞, a)
(-∞, ∞)
The absolute value of a number is
A) always positive
B) always an integer
C) never a fraction
D) never negative
Interpret the following geometrically. Represent your
solution on the number
line and in set notation.
EX4: | x | = 5
EX5: | x | = -3
EX6: | x - 1 | = 4
EX7: | x+ 1 | = 4
EX8. Write an absolute value equation corresponding to the following graph
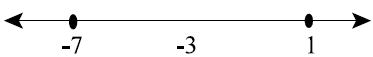
The geometric meaning of | x - a | = b where b > 0 is
The algebraic solution of absolute value
equations of the form | x - a | = b is
EX9: Solve and graph. | 2x - 3 | = 7
EX10: Solve and graph | x - 7 | < 2
EX11: Solve and graph | x + 5 | < -3
The geometric meaning of absolute value
inequalities of the form
| x - a | < b is
The algebraic solution of absolute value
inequalities of the form
| x - a | < b is
EX12: Solve and graph | 3 - 2x |≤ 5.
EX13: What set of numbers is described by | x - 1 | > 4?
EX14: Solve and graph | x - 3 | ≤ 2
EX15: Solve and graph | x + 4 | > -3
The geometric meaning of absolute value
inequalities of the form
| x - a | > b is
The algebraic solution of absolute value
inequalities of the form
| x - a | > b is
EX16: Solve and graph | 2x - 5 | ≥ 8
EX17: Graph y = | x |
EX18: Graph y = | x - 2 | + 3
EX19: Solve | x - 3 | = | 2x + 5 | and check your answer(s).
EX20: A car CD player has an operating temperature of | t
- 40° | ≤ 80°
where t is the temperature in degrees Fahrenheit. Solve for t and
give the range of operating temperatures for the CD player.
Chapter 5, Sect. 1: Polynomials and Polynomial
Functions
Def. Algebraic terms - expressions that contain constants
and/or variables
Examples:
Def. Polynomial – the sum of one or more algebraic terms
whose variables
have whole number exponents
Examples:
Def. Monomial –
Examples:
Def. Binomial –
Examples:
Def. Trinomial –
Examples
Def. If a ≠ 0, the degree of a^n is n. The degree of a
monomial containing
several variables is the sum of the exponents of those variables. The
degree of a polynomial is equal to the degree of its highest degree
term.
Examples:
Note 1: The degree of a nonzero constant is 0.
Explanation:
Note 2: The degree of 0 is indeterminate.
Explanation.
Graphs of Special Functions:
| Linear Function |
Squaring Function |
| EX. y = 2x + 1 |
EX. y = x2 |
Domain
Range |
Domain
Range |
| Cubing Function |
Absolute Value Function |
| EX. y = x3 |
EX. y = |x| |
Domain
Range |
Domain
Range |
EX1: Write -x2 + 3x5 - 7x + 3x3 in (A) descending order and
(B) in ascending order
Descending order:
Ascending order:
EX2: If P(x) = 3x2 - 2x + 1, find P(-4), P(½), and P(n).
EX3: The height, h, in feet, of a ball shot straight up
with an initial velocity
of 64 feet per second is given by the polynomial function
h(t) = -16t2 + 64t
Find the height of the ball in (A)3 seconds and (B)in 1.78 seconds.
EX4: The number of feet that a car travels before stopping
depends on the
driver’s reaction time and braking distance. For a certain driver, the
stopping distance is given by d(v) = 0.04v2 + 0.93v where v is
the speed of the car in mph. Find the stopping distance if the speed of
the car is (A) 35 mph, (B) 55 mph, and (C) 70.86 mph.
|