Equations and Inequalities

1.1 Linear Equations

An equation where the greatest degree of the variable is 1 is said to be a linear equation or a first-degree equation.
example: y = 3x + 5

The graph of a linear equation is a ___________________.

An equation that is true for every value of the variable is called an ________________.
example: 2x+8 = 2(x + 4)

An equation that is true for some values of the variable but not others is called a ___________________ equation.
example: 3x + 5 = 8

An equation that has no solution is called a ______________________.
example: x = x + 3

Page 90: 2, 8, 14, 20, 25, 28, 30, 36

Solving for a specified Variable (Literal Equations)
Equations such as formulas where the solution relates several variables is called a ___________________.
example: Simple Interest formula I = Prt
Page 91: 40, 46, 54, 59, 70

1.2 Applications and Modeling with Linear Equations

Read ‘Solving an applied problem’ on page 93.
Geometry problems
Page 101: 10, 16

Motion or Distance Problems
Read ‘Problem Solving’ on page 94.
Page 102: 20, 28

Work Rate Problems
Read ‘Problem Solving’ on page 95.
Page 104: 31, 34

Mixture Problems
Read ‘Problem Solving’ on page 96.
Page 104: 37, 40

Investment Problems
Read ‘Problem Solving’ on page 98.
Page 105: 43, 46

Modeling with Linear Equations
A ______________________ is an equation or inequality that describes a relationship between two quantities.
Page 105: 49, 52

1.3 Complex Numbers

A complex number is represented in the form a + bi where a and b are real numbers and i is the imaginary number defined as

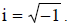
In other words the square root or an even root of a negative number which we thus far said was undefined or ‘cannot be
expressed as a real number’ can now be defined using the imaginary number i.
example:
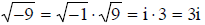
If
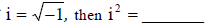
Therefore the real number system that comprises of

is a subset of the complex number system.

Arithmetic operations like addition, subtraction, multiplication, and division with complex numbers work the same way like they
do for real numbers. Just remember to keep the real parts and imaginary parts separate and to substitute ___________ for i² .
Page 114: 19, 23, 26, 35, 38, 44, 50, 54, 62, 70, 88, 94

1.4 Quadratic Equations

An equation that can be expressed in the form ax² + bx + c = 0 , where a, b and c are real numbers with a ≠ 0 , is a quadratic
equation.
The degree of the variable in a quadratic equation is 2.

Zero-Factor Property or the Principle of zero products
If a and b are complex numbers with a × b = 0,then a = 0 or b = 0 or both a and b equal 0.
Page 124: 14, 19

Square Root Property
If x² = k,then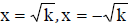
Page 124: 22, 24, 30

Completing the Square
Read ‘Solving a quadratic equation by completing the square’ on page 117.
Page 124: 32, 40

The Quadratic Formula
The solutions of the quadratic equation ax² + bx + c = 0, where a≠0 are
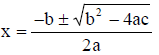
Page 124: 46, 52

Solve for a specified variable
Page 124: 68

The Discriminant
The quantity under the radical in the quadratic formula ______________, is called the discriminant. Based on its value we can
identify the nature of the solutions of the quadratic equation.
If the dicriminant is 0, the quadratic equation has one real number solution.
If the dicriminant is positive, the quadratic equation has two real number solutions.
If the dicriminant is negative, the quadratic equation has two imaginary solutions.
Page 125: 78

Finding the quadratic equation whose solutions are given
Page 125: 84

1.5 Applications and Modeling with Quadratic Equations

Read ‘Problem Solving’ on page 125.

Geometry Problems
Page 131: 4, 6, 10

Using the Pythagorean Theorem
Read ‘Pythagorean Theorem’ on page 127.
Page 132: 18, 24

Finding the height of a propelled object
Read ‘Height of a Propelled Object’ on page 128.
Page 133: 28, 30

Modeling with Quadratic Equations
Page 135: 36

1.6 Other Types of Equations

Rational Equations
Read ‘Rational Equations’ on page 136.
Page 144: 8, 14, 26

Equations with Radicals
Read ‘Power Property’ on page 138.
Read ‘Solving an Equation involving Radicals ’ on page 139.
Page 144: 28, 54, 38

Equations Quadratic in Form
Read ‘Equations Quadratic in Form’ on page 141.
Page 145: 62, 64

1.7 Inequalities

An inequality is an equation where the = sign is replaced by one of the following symbols: >,≥,<,≤,≠
Example: x + 5 < 3
The values of the variable that satisfy the inequality form the solution set of the inequality.

Read ‘Properties of Inequalities’ on page 147
Page 156: 14, 16
Note: Arithmetic operations on inequalities, work the same way as they do for equations EXCEPT when multiplied or divided
by a negative number. Then the sign of the inequality changes.

Read ‘Linear Inequality in one Variable’ on page 147.
Refer to the table on page 148.
Page 156: 22, 24

Three-part Inequality or Double Inequality
Page 156: 32, 34

A product will break-even or begin to produce a profit, only if the revenue from selling the product at least equals the cost of
producing it. If R represents revenue and C is the cost, then the break-even point is the point where R = C.
Page 157: 38

Quadratic Inequalities (MAKE A SIGN CHART)
Read ‘Quadratic Inequalities’ on page 150.
Consider the quadratic inequality x² - x - 12 < 0

Read ‘Solving a Quadratic Inequality’ on page 150.

Page 157: 44, 50

Higher Degree Inequalities(MAKE A SIGN CHART)
Page 158: 66, 68

Application
Page 159: 96