SOLVING LINEAR AND QUADRATIC EQUATIONS
Square Root Method - All quadratic equations can be
solved by this method. However, we might
want to avoid this method for some quadratic equations because it can get very
cumbersome.
•Isolate the squared term on one side of the equation. Be
sure its coefficient is a positive 1 !!!!!!
•Apply the Square Root Property.
•If necessary, further isolate the variable.
Following are two examples for which the Square Root
Methods works well:
Example 1:
Solve 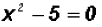 . Find real
solutions only! . Find real
solutions only!
Isolate the squared term
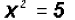
and use the Square Root Property
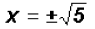
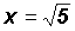 or or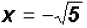
The real solutions are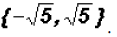
Example 2:
Solve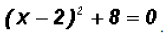 . Find real
solutions only! . Find real
solutions only!
Isolate the squared term
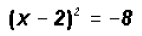
use the Square Root Property
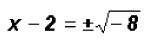
and further isolate the variable
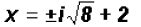
Simplify the radical
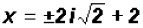
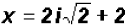 or or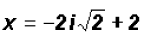
There are NO real solutions.
Example 3:
Solve 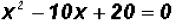 . Find real
solutions only! . Find real
solutions only!
Let's use the Square Completion Method to help us solve
the equation by the Square
Root Method.
Notice that our equation has three terms, but it is not a
Perfect Square Trinomial. We will
use 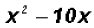 for our Perfect Square Trinomial. The
middle term is for our Perfect Square Trinomial. The
middle term is 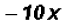 . .
Procedure
1. Divide the coefficient of the middle term by 2: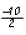
2. Raise to the second power: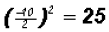 . We have just found the third term
. We have just found the third term
of the Perfect Square Trinomial!
3. Insert the third term into the given equation, however,
in order not to
CHANGE THE VALUE OF THE EQUATION we also have to subtract the
inserted value as follows:
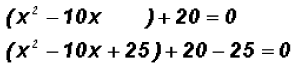
4. Lastly, we factor:
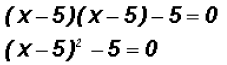
Now we can solve the equation using the Square Root Method
as follows:
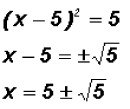
The real solutions are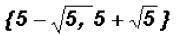
|