Review Solving Quadratic Equations

Topic 1-1: Review Solving Quadratic Equations

Three methods to solve equations of the
form ax² + bx + c = 0.

1. Factoring the expression and applying the
Zero Product Property
2. Completing the square and applying the
Property of Square Roots
3. Applying the Quadratic Formula

Ex. Solve by factoring and applying the
Zero Product Property.

x² + 2x − 48 = 0

Ex. Solve by completing the square and
applying the Property of Square Roots.

x² + 6x + 2 = 0

Ex. Solve by applying the Quadratic
Formula.
2x² − 4x −1= 0

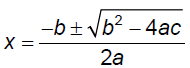
Ex. Solve by each of the previous two
methods.
x² − 8x + 4 = 0

Topic 1-2: Solving Equations by Factoring

The next three equations can be solved after a
GCF is factored out of the expression.

Ex. 1 Solve.
x⁵ = 64x²

Ex. 2 Solve.
x⁵ + 3x⁴ −10x³ = 0

Ex. 3 Solve.

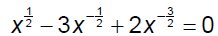
The next three equations are described as
quadratic-type when an appropriate substitution is
applied.

Ex. 1 Solve.
( 2x − 1)² − 7(2x − 1) + 6 =  0

Ex. 2 Solve.
x⁴ −10x² + 9 = 0

Ex. 3 Solve.

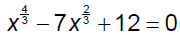
The next two equations involve expressions that
are factorable by the grouping method.

Ex. 1 Solve.
2x³ + x² −18x − 9 = 0

Ex. 2 Solve.
x³ − 2x² − 3x + 6 = 0

Topic 1-3a: Radical Equations

Radical equations have one or more radical
expressions in the equation. To solve, isolate a
radical on one side and then square both sides.
Solve the resulting equations and check your
solutions.

Ex. 1 Solve.

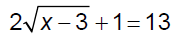
Point of emphasis: Solving a radical equation by this
method tends to create “extraneous”
solutions so you must always check
your results.

Ex. 2 Solve.

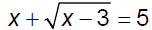
Ex. 3 Solve.

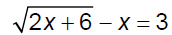
Topic 1-3b: Rational Equations

Rational equations have one or more rational
expressions in the equation. To solve, find the
least common denominator and multiply the LCD to
both sides of the equation. Solve the resulting
equation and check your results.

Ex. 1 Solve.

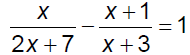
Ex. 2 Solve.

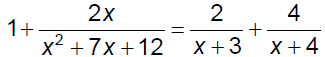
Topic 1-3c: Absolute Value Equations

For the equation |x|= c, there are three cases to
consider:
If c > 0, then the solutions can be found by x = ±c.
If c = 0, then the solutions can be found by x = 0.
If c < 0, then there are no solutions.

Ex. 1 Solve.
|4x − 5| = 9

As necessary, take steps to isolate the absolute
value expression on one side before applying the
previous rule.

Ex. 2 Solve.

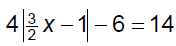
Ex. 3 Solve.

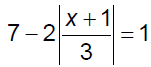
Topic 1-4: Linear & Compound Inequalities;
Interval Notation

Inequalities, like equations, are statements of
relationships.

Equations state that two expressions are equal
while inequalities state that expressions are not
necessarily equal.

Solving linear inequalities and solving linear
equations require similar techniques with the
familiar appendant that multiplying or dividing by a
negative causes the inequality to reverse.

Ex. 1 Solve.
3(5 − 2x) ≥ 1

Ex. 2 Solve.

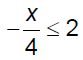
Ex. 3 Solve.
3x ≥ −18

One significant difference is in the solution set.
Equations typically have distinct, discrete values in
their solution set. Inequalities, on the other hand,
typically have continuous intervals of solutions.

We graph inequalities on a number line so that we
can “see” the solution set.

To graph the solution set of an inequality:

Mark the boundary value(s) of the solution interval. At each
boundary value, note the inclusion or exclusion of the
boundary in the solution set.

If the boundary is included, use a closed dot ●
If the boundary is excluded, use an open dot ○

Shade appropriately using test values to identify the intervals.
Interval notation allows us to identify a continuous
interval of values. We often associate interval
notation with inequalities since the solution sets of
inequalities are usually continuous intervals.

Interval Notation

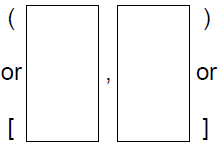		parentheses – boundary excluded
		brackets –  boundary included
left end boundary or − ∞	right end boundary or ∞

Sketch the graph of the inequality on the number
line and write the corresponding interval of values
in interval notation.

Ex. 1
x ≥ 3

Ex.
2 x < −1

Ex. 3
 −4 < x ≤ 0

Ex. 4
1< x < 15

Symbols/terminology relevant to intervals & interval
notation:

Closed Interval: [2,7]
both numeric boundaries included

Open Interval: (−4,3)
both numeric boundaries excluded

Half-open Interval: [−5,−1), (0,4]
one end open, one end closed

Infinite Interval: (−∞,4), [5,∞), (−∞,∞)
unbounded on one or both ends

Union Symbol: ∪ <means or>
each entire interval appropriate

Intersection Symbol: ∩ <means and>
only common (i.e. overlapping) interval appropriate

Compound Inequalities (also known as
Simultaneous or Three-Part Inequalities)

Ex. Solve. Present solutions graphically &
in interval notation.

−5 < 2x −1≤ 13

Points for observation:

It is often possible to solve a compound inequality
be applying a common step to all three parts of the
inequality.

Certain compound inequalities must be rewritten as
follows to be solved:

A < B < C implies that A < B and B < C

Topic 1-5a: Absolute Value Inequalities:
the less than case

If |x| < c, then − c < x < c.
(correspondingly true for ≤)

Ex. 1 Solve. Present solutions graphically &
in interval notation.

|3x − 2| < 5

As with absolute value equations, with absolute
value inequalities you want to isolate the absolute
value expression.

Ex. 2 Solve. Present solutions graphically &
in interval notation.

5 − 3| x + 2| ≥ −13

Ex. 3 Solve. Present solutions graphically &
in interval notation.
|2x −1 |+ 4 ≤ 17

Topic 1-5b: Absolute Value Inequalities:
the greater than case

If |x |> c, thenx < −c or x > c.
(correspondingly true for ≥)

Ex. 1 Solve. Present solutions graphically &
in interval notation.
|4x − 5 |> 7

Ex. 2 Solve. Present solutions graphically &
in interval notation.
5 + 2 |x + 3| ≥ 13

Exceptional Scenarios

Ex. 1 Solve.
|2x − 9 |≤ −3

Ex. 2 Solve.
|2x − 9| ≤ 0

Ex. 3 Solve.
|2x − 9| > −3

Ex. 4 Solve.
|2x − 9 |> 0

Topic 1-6: Nonlinear Inequalities

A nonlinear inequality is an inequality statement
that cannot be expressed using a linear expression.
Whereas linear inequalities can be solved in a
straight-forward fashion, nonlinear inequalities must
be approached differently.

We will investigate three cases of nonlinear
inequalities:

1. Polynomial inequalities (product case)
2. Rational inequalities, one side is zero (simple quotient
case)
3. Rational inequalities, both sides are nonzero (quotient
rewrite case)

Case 1: Polynomial Inequalities

Process:

1. As necessary, rewrite the inequality so that one side
is 0.
2. Factor the polynomial.
3. Set each factor equal to zero and solve. These
solutions will be the boundary values of the
polynomial inequality.
4. Draw a number line and mark boundary values with
an appropriate dot.
5. Pick a test value from each interval formed by the
boundary values.
6. Create a chart with columns for each interval and
rows for each factor plus the overall expression
being compared to zero.
7. Use the test values to determine if each factor is
positive or negative over a given interval. Then use
these signs to determine whether the overall
expression is positive or negative over a given
interval.
8. Shade appropriately. (Positive > 0, Negative < 0)
9. Identify the solution intervals from the graph.

Ex. 1 Solve. Present solutions graphically &
in interval notation.
(2x +1)(x − 4) ≥ 0

Ex. 2 Solve. Present solutions graphically &
in interval notation.
x³ + 5x² −14x ≤ 0

Ex. 3 Solve. Present solutions graphically &
in interval notation.
x³ − 2x² − 4x + 8 > 0

Ex. 4 Solve. Present solutions graphically &
in interval notation.
25x ≥ x³

Case 2: Rational Inequalities, one side is zero

Case 2 is almost exactly the same as case 1. In fact the
same set of directions can be applied if the following
instructions are added:

2. Factor the numerator and denominator, as possible
3a. Boundary values established by factors from the
denominator are always excluded from the solution
set and on the number line the boundary must be
represented by an open dot regardless of the
inequality symbol involved.

Ex. 1 Analyze.

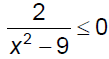
Ex. 2 Solve. Present solutions graphically &
in interval notation.

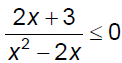
Case 3: Rational Inequalities, both sides are
nonzero

Case 3 can be rewritten into a case 2 scenario. This requires
moving all expressions to one side, finding an LCD, and
combining all the expressions into one fraction.

Ex. 1 Solve. Present solutions graphically &
in interval notation.

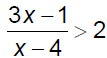
Ex. 2 Solve. Present solutions graphically &
in interval notation.
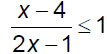