The Quadratic Equation
8.4 The Discriminate
Need To Know
▪ Review the Quadratic Formula
▪ The Discriminate
▪ Predicting roots
▪ Writing equations from solutions
The Quadratic Formula
For ax2 + bx + c = 0,
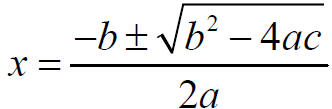
The Discriminate is ________________
The Discriminate
| Discriminate |
Nature of Solutions |
| 0 |
|
Positive –
Perfect Squar |
|
Positive –
Not a perfect |
|
| Negative |
|
Predicting the Solution Type
Determine what type of solution each has.
x2 – 7x + 5 = 0
x2 + 4x + 6 = 0
9t2 – 48t + 64 = 0
end
8.6 Graphing the Quadratic Eq.
Need To Know
▪ Graph quadratic equation
▪ Finding the vertex and axis of symmetry
▪ Vertex Form of an equation
Graph f (x) = ax2: The effect of “a”?
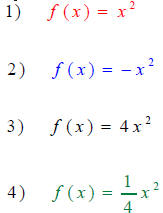 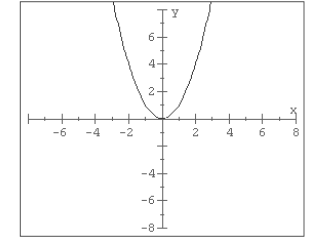 Label
vertex point, use axis of sym. Label
vertex point, use axis of sym.
Observation:
a > 1, then parabola is _________
a < 1, then parabola is _________
a < 0, then parabola is _________
The Graph of f (x) = a(x – h)2
Graph:
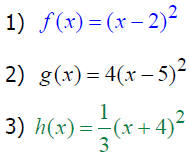  Label
vertex point, use axis of sym. Label
vertex point, use axis of sym.
Observation:
(x+h) h is neg, then parabola _________
(x–h) h is pos, then parabola _________
The effect of h is _________
The Graph of f (x) = a(x – h)2 + k
Graph:
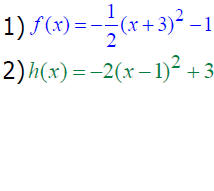  Label
vertex point, use axis of sym. Label
vertex point, use axis of sym.
Observation:
The vertex is _________
The equation of the A.O.S. _________
The effect of k _________
Graphing y = a(x – h)2 + k
Graph:
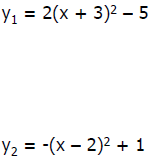 
Summarize the Vertex Form
y = a(x – h)2 + k is the Vertex Form.
Three parameters: a, h, k
Maximum or Minimum
end
8.7 More about Graphing Quadratics
Need To Know
▪ Review completing the square
▪ Converting into Vertex Form
(not to learn but to appreciate the short cut formula)
▪ Vertex Point Formula – Short Cut
▪ Finding intercepts
▪ Sketching the graph of a quadratic
Completing the Square
Recall:
x2 – 10x + _______ =
Recall:
y = a(x – h)2 + k
What is the vertex point? ____________
Convert Quadratics to Vertex Form
If the quadratic is in standard form, we have no
information.
We need to change the form into vertex form (squared stuff).
g(x) = x2 – 10x + 21
f(x) = 4x2 + 8x - 3
Vertex Point – short cut (easy way)
If f(x) = ax2 + bx + c, then (h, k) = ___________
which means _____________________________.
1. Find h with the formula
2. Find k by plugging h into the function.
g(x) = x2 – 10x + 21
f(x) = 4x2 + 8x – 3
Intercept Points
Recall:
X-intercept point = point where graph crosses x-axis. (a, 0)
Find the x-intercept point by letting y = 0.
Y-intercept point = point where graph crosses y-axis. (0,
b)
Find the y-intercept point by letting x = 0.
Example:
Find the intercepts of f(x) = x2 + 5x – 6
Sketch Graph
y = x2 + 6x + 5
Label vertex point,
Label intercept points
Sketch Graph
y = -3x2 + 6x + 2
Label vertex point,
Label intercept points
end
|