Solving Linear Equations
Consider the equation:
3x − 5 =13
We are undoing what is happening to x ( Multiplication by 3 and subtraction
by 5 ) . So we undo by going backwards: undo subtraction of 5 and then
undo multiplication by 3.
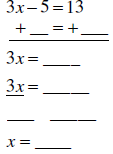
Any equation that can be written in the form ax + b = c is called a linear
equation. In this section all of the equations are linear. To solve
linear
equations:
1.) Simplify both sides of the equation.
2.) Collect all the variable terms and all constant terms on the
other side.
3.) Isolate the variable and solve.
4.) Then check the answer.
EXAMPLE: Solve and Check
To Solve 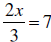 we can do two
things: we can do two
things:
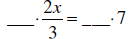 multiply by 3 or multiply by 3 or
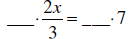 multiply by multiply by
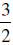
2x = ____ divide by 2 x = ____
x = ___
EXAMPLE: Solve and Check
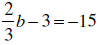
Sometimes it may be necessary to simplify before trying to solve. We get all
the x 's together and the constants together before we solve.
EXAMPLE: Solve and Check
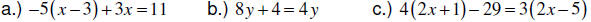
Many people would love to do away with having to deal with
fractions. When
an equation has fractions involved, we may use the multiplication property of
equality to clear the fractions. We multiply both sides by the LCD.
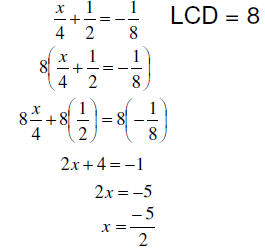
Therefore we don’t need to
deal with fractions very much.
EXAMPLE: Solve:
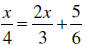
IDENTITIES AND IMPOSSIBLE EQUATIONS:
The equations that we have been solving are called conditional equations
because they only work for one number. An equation that is true for all values
of its variable is called an identity.
3( x + 2) = 3x + 6 is an identity
2x + 2 = 2x + 3 is an equation that is never true.
Solve the above equation to see what happens:

EXAMPLE: Solve the equation.
| a.) −3( s + 2) = −2( s + 4) − s |
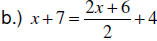 |
EXAMPLE: A driver left the plant
with 300 bottles of drinking water on
his truck. His route consisted of
office buildings, each of which
received 3 bottles of water. The
driver returned to the plant with 117
bottles on the truck. To how many
office buildings did he deliver? |
EXAMPLE: The formula: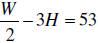
models the recommended weight, W ,
in pounds, for a male, where H
represents the man’s height , in inches,
over 5 feet. What is the recommended
weight for a man who is 6 feet, 3
inches tall? |
|