Quadratic and Rational Inequalities
A quadratic inequality is any
inequality that can be put in
one of the forms
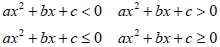
where a, b, and c are real numbers and a≠0.
Solving Quadratic Inequalities
 Step 1: write the inequality in standard
form. Step 1: write the inequality in standard
form.
 Step 2: solve the related quadratic equation. Step 2: solve the related quadratic equation.
 Step 3: locate the boundary points on a Step 3: locate the boundary points on a
number line.
 Step 4: construct a sign chart. Step 4: construct a sign chart.
 Step 5: the solution set is the interval that Step 5: the solution set is the interval that
produced a true statement.
Example 1: Solve a Quadratic
Inequality
Solve: 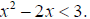
Solution:
Step 1: Write the inequality in
standard form.
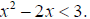
Step 2: Solve the related quadratic equation.
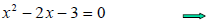
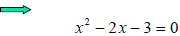
(x-1)(x-3)=0
x+1=0 or x-3=0
x=-1 or x= 3
The boundary points are -1 and 3.
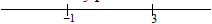
These two points divide the number
line into three test intervals, namely
(−∞,-1) ,(−1,3) ,and (3,∞) .
Take a test point within each
interval and check the sign.
Test
Interval |
Test
Point |
X+1 |
X-3 |
(x+1)(x-3) |
| (−∞,-1) |
-2 |
- |
- |
+> 0 |
| (−1,3) |
0 |
+ |
+ |
-< 0 |
| (3,∞) |
4 |
+ |
+ |
+>0 |

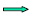
The question is "where
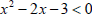 ?" ?"
Our table shows that
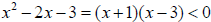
in the interval (-1,3).
So the solution set is
the interval (-1,3)
Practice Exercises
Solving Rational Inequalities
Solve: 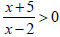
It is incorrect to multiply both sides by
x-2 to clear fractions. The problem is
that x-2 contains a variable and can be
positive or negative, depending on the
value of x. Thus, we do not know
whether or not to reverse the sense of
inequality.
Example 2: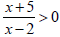
solution: We begin by finding values
of that make the numerator and
denominator 0
Set the numerator and denominator equal to 0.

Solve
x=-5 and x=2
The boundary points are -5 and 2.
Locate boundary points -5 and 2
on a number line.

These boundary points divide the
number line into three intervals,
namely (−∞,-5),(-5,2), and (2,∞).
Now, construct a sign chart: take
one test point from each interval
and check the signs.


| Intervals |
Test
Points |
x+5 |
x-2 |
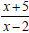 |
| (−∞,-5) |
-6 |
- |
- |
+> 0 |
| (-5,2) |
0 |
+ |
- |
-< 0 |
| (2,∞) |
3 |
+ |
+ |
+>0 |
The given question is "for what values
of the quantity 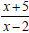 is
positive?" is
positive?"
Our table shows that
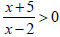 for for
(−∞,-5) or (2,∞).
Thus the solution set is
(−∞,-5) or (2,∞).
The graph of the solution set on a
number line is shown as follows:
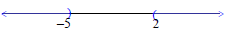
Practice Exercises
| Solve: |
Answers: |
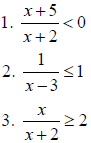 |
(-5,-2)
(−∞,3) or [4,∞)
[-4,-2] |
|