Systems of Linear Equations: Cramer's Rule
Definition: Every square n × n matrix A has a real number associated
with it called the
determinant of A, denoted by |A|.
Definition: Determinant of a 2 × 2matrix:
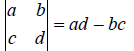
Example (1) : Evaluate
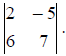
solution :
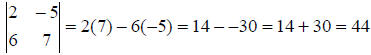
Definition: The minor Mij of a square n × n matrix A is the determinant of the
matrix
found by deleting the ith row and jth column of A.
Example (2): Evaluate M23 where

solution : Delete the second row and third column then
evaluate the determinant of the
resulting 2 × 2 matrix.
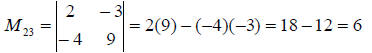
Definition: Determinant of a 3× 3 matrix:
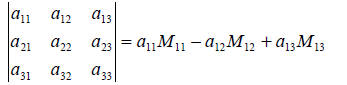
Example (3): Evaluate the determinant of the matrix from
example (2)
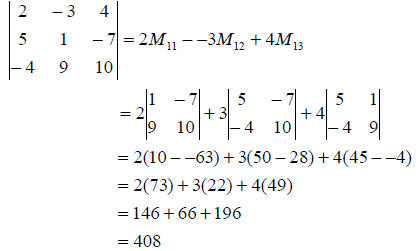
In example (3) we calculated the determinant by expanding
across the first row. We can
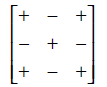
calculate the determinant by expanding across any row or any column by using the
following sign array.
Example (4): Calculate the following determinant by
expanding across the second
column.
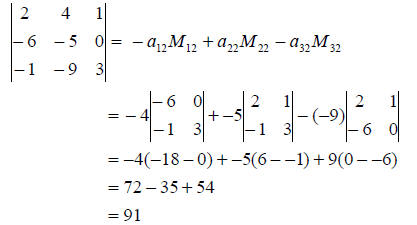
Note: When calculating the determinant it is always best
to expand about the row or
column with the greatest number of 0’s.
Theorem: Cramer’s Rule for Two Equations and Two Variables
The solution to the system of equations
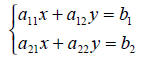
is given by
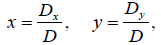 provided D ≠ 0 provided D ≠ 0
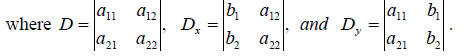
Examples: Solve using Cramer’s Rule:
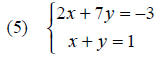
solution :
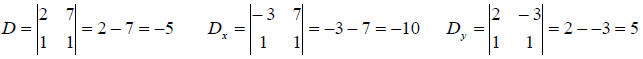
the solution to the system is given by
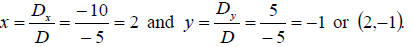
A similar procedure is used for solving a system of three
equations and three variables.
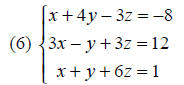
solution :
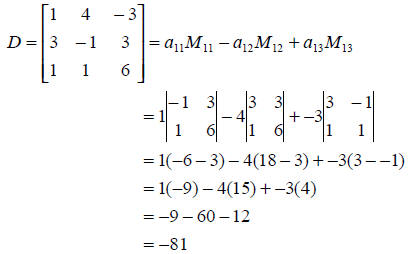
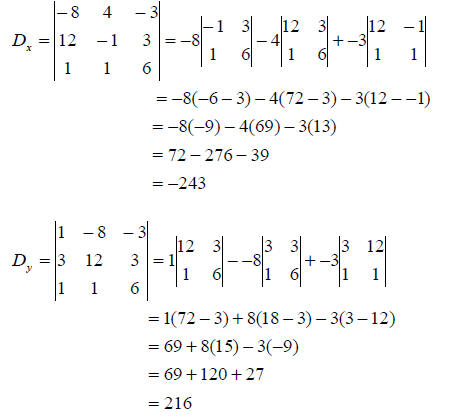
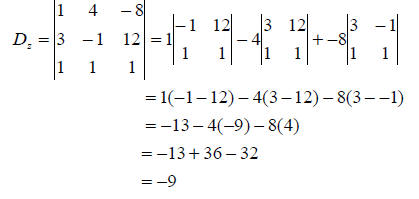
The solution is
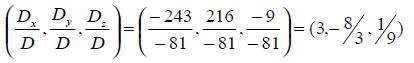
|